Rekurze

Ahoj, rekurze!

Rekurzi jsme stručně zmínili v předchozí kapitole. V této kapitole se na ni podíváme zblízka, proč je v Haskellu tak důležitá a jak můžeme najít velice výstižná a elegantní řešení problémů díky rekurzivnímu myšlení.

Pokud stále ještě nevíte, co to rekurze je, přečtěte si tuhle větu. Ha, ha! Dělám si legraci! Rekurze je ve skutečnosti způsob definování funkce, ve kterém je použita tatáž funkce ve své vlastní definici. Definice v matematice jsou často zadány rekurzivně. Například fibonacciho posloupnost je definována rekurzivně. Nejprve si definujeme první dvě fibonacciho čísla nerekurzivně. Řekneme, že F(0) = 0 a F(1) = 1, což znamená, že nulté a první fibonacciho číslo je nula a jednička (v tomto pořadí). Poté prohlásíme, že pro ostatní přirozená čísla je fibonacciho číslo součet dvou předchozích fibonacciho čísel. Takže F(n) = F(n-1) + F(n-2). Tím pádem F(3) je F(2) + F(1), což je (F(1) + F(0)) + F(1). Protože jsme se dostali k nerekurzivně definovaným fibonacciho číslům, můžeme bezpečně říct, že F(3) se rovná 2. Nerekurzivně definované části rekurzivních definicí (stejně jako bylo tady F(0) a F(1)) se také říká okrajová podmínka a je dost důležitá, jestliže chceme, aby naše rekurzivní funkce někdy skončila. Kdybychom neměli definované F(0) a F(1) nerekurzivně, nikdy bychom nedostali řešení pro jakékoliv číslo, protože bychom po dosažení nuly šli do záporných čísel. Z ničeho nic bychom tvrdili, že F(-2000) je F(-2001) + F(-2002) a konec by byl stále v nedohlednu!

Rekurze je v Haskellu důležitá, protože na rozdíl od imperativních jazyků provádíme výpočty deklarováním něčeho, jaké to je, místo deklarování jak to dostat. To je důvod, proč v Haskellu nejsou žádné while nebo for smyčky a místo toho jsme museli mnohokrát použít rekurzi pro deklaraci něčeho, jaké to je.

Maximální skvělost

Funkce maximum vezme seznam věcí, které se dají uspořádat (např. instance typové třídy Ord) a vrátí největší z nich. Přemýšlejte, jak byste to napsali imperativním stylem. Pravděpodobně byste si vytvořili proměnnou, aby uchovávala aktuální maximální hodnotu a poté byste postupně procházeli seznam a pokud by byl prvek v seznamu větší než současná nejvyšší hodnota, nahradili byste to tím prvkem. Maximální hodnota, která by zbyla na konci, by byla výsledek. Páni! To jsme použili celkem dost slov na popsání tak jednoduchého algoritmu!

A teď se podíváme, jak bychom to definovali rekurzivně. Mohli bychom nejprve vytvořit okrajovou podmínku a prohlásit, že maximum z jednoprvkového seznamu se rovná tomu prvku z něj. Pak můžeme říct, že maximum z delšího seznamu je první prvek, pokud je ten prvek větší než maximum ze zbytku. Jestliže je maximum ze zbytku větší, tak je výsledek maximum ze zbytku. Takhle to je! A teď si to napíšeme v Haskellu.

maximum' :: (Ord a) => [a] -> a
maximum' [] = error "maximum z prázdného seznamu"
maximum' [x] = x
maximum' (x:xs)
    | x > maxTail = x
    | otherwise = maxTail
    where maxTail = maximum' xs

Jak můžete vidět, vzory se dobře snášejí s rekurzí! Většina imperativních jazyků neobsahuje vzory, takže musíte vytvořit hromadu if a else na otestování okrajových podmínek. Zde je jednoduše zahrneme do vzorů. Tedy první okrajová podmínka říká, že jestliže je seznam prázdný, spadni! To dává smysl, protože co je maximum z prázdného seznamu? Nevím. Druhý vzor také zastává okrajovou podmínku. Říká, že jestliže to je jednoprvkový seznam, prostě vrať ten jediný prvek.

A třetí vzor je ten, ve kterém se všechno děje. Použili jsme vzor na rozdělení seznamu na první prvek a zbytek. Tohle je běžný postup při provádění rekurze na seznamech, na který je potřeba si zvyknout. Použijeme konstrukci where pro definování maxima zbytku seznamu maxTail. Poté zkontrolujeme, jestli je první prvek větší než maximum ze zbytku seznamu. Jestliže je, vrátíme ho. V opačném případě vrátíme maximum ze zbytku seznamu.

Zkusíme vzít na ukázku nějaký seznam čísel, třeba [2,5,1], a zjistit, jak by to s ním mohlo fungovat. Jestliže na něj zavoláme funkci maximum', první dva vzory nebudou sedět. Třetí ovšem ano a rozdělí seznam na 2 a [5,1]. Klauzule where chce znát maximum z [5,1], takže následujme tuhle cestu. Znovu se to zastaví u třetího vzoru a [5,1] se rozdělí na 5 a [1]. Klauzule where chce znovu znát nejvyšší číslo ze seznamu [1]. Protože to je okrajová podmínka, vrátí 1. Konečně! Takže když postoupíme o krok dál porovnáním čísla 5 s maximem z [1] (což je 1), dostaneme zpátky 5. Víme tedy, že maximum z [5,1] je 5. Postoupíme zase o krok dál, kde máme 2 a [5,1]. Porovnáním čísla 2 s maximem z [5,1], což je 5, se rozhodneme pro číslo 5.

Čistější způsob, jak napsat tuhle funkci, je použít max. Pokud si pamatujete, max je funkce, která vezme dvě čísla a vrátí větší z nich. Tady je ukázka, jak bychom mohli přepsat maximum' za použití funkce max:

maximum' :: (Ord a) => [a] -> a
maximum' [] = error "maximum z prázdného seznamu"
maximum' [x] = x
maximum' (x:xs) = max x (maximum' xs)

To je ale elegantní! Maximum ze seznamu je v podstatě max z prvního prvku a maxima ze zbytku.

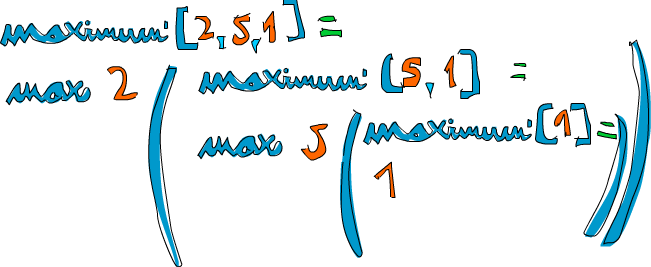
Několik dalších rekurzivních funkcí

A teď, když víme, jak se zhruba dá myslet rekurzivně, napišme si pár funkcí s použitím rekurze. Nejprve si implementujeme funkci replicate. Tato funkce vezme parametr typu Int a nějaký prvek a vrátí seznam, který má několik opakování toho stejného prvku. Kupříkladu replicate 3 5 vrátí [5,5,5]. Zamysleme se nad okrajovou podmínkou. Můj tip je, že okrajová podmínka je 0 nebo méně. Jestliže zkusíme opakovat něco nulakrát, měl by se vrátit prázdný seznam. Stejně pro záporná čísla, protože to nedává moc smysl.

replicate' :: (Num i, Ord i) => i -> a -> [a]
replicate' n x
    | n <= 0    = []
    | otherwise = x:replicate' (n-1) x

Použili jsme stráže místo vzorů, protože testujeme booleovskou podmínku. Jestliže je n menší nebo rovno 0, vrátí se prázdný seznam. Jinak vrátí seznam, který má x jako první prvek a poté x opakované n mínus jedenkrát jako zbytek. Část s (n-1) způsobí, že naše funkce nakonec dosáhne okrajové podmínky.

Dále si vytvoříme funkci take. Ta vezme určitý počet prvků ze seznamu. Například výraz take 3 [5,4,3,2,1] vrátí seznam [5,4,3]. Jestliže zkusíme vzít 0 nebo méně prvků ze seznamu, dostaneme prázdný seznam. Stejně pokud zkusíme vybrat něco z prázdného seznamu, dostaneme prázdný seznam. Všimněte si, že tohle jsou dvě okrajové podmínky. Takže to zkusíme zapsat:

take' :: (Num i, Ord i) => i -> [a] -> [a]
take' n _
    | n <= 0   = []
take' _ []     = []
take' n (x:xs) = x : take' (n-1) xs

První vzor uvádí, že pokud zkusíme vzít 0 nebo záporný počet prvků, dostaneme prázdný seznam. Všimněte si, že jsme použili _ na ověření seznamu, protože nás v tomhle případě ten seznam nezajímá. Také si všimněte použití stráže bez části otherwise. Jestliže se tím pádem ukáže, že n je větší než 0, ověření selže a přejde se na další vzor. Druhý vzor naznačuje, že pokud chceme vzít cokoliv z prázdného sezamu, dostaneme prázdný seznam. Třetí vzor rozdělí seznam na první prvek a zbytek. A poté uvedeme, že když vezmeme n prvků ze seznamu, je to stejné jako sezam, který obsahuje první prvek x a poté seznam n-1 prvků ze zbytku. Zkuste si vzít kus papíru, abyste si zapsali, jak by mohlo vypadat vyhodnocování, řekněme, tří prvků ze seznamu [4,3,2,1].

Funkce reverse jednoduše převrátí seznam. Zamyslete se nad okrajovou podmínkou. Jaká je? No tak… je to prázdný seznam! Převrácený prázdný seznam je stejný jako prázdný seznam. Tak jo. A co s ostatními případy? No, můžeme říct, že když rozdělíme seznam na jeho první prvek a zbytek, převrácený seznam je stejný jako převrácený zbytek a k němu na konec přidaný první prvek.

reverse' :: [a] -> [a]
reverse' [] = []
reverse' (x:xs) = reverse' xs ++ [x]

A je to!

Protože Haskell podporuje nekonečné seznamy, naše rekurze nemusí mít okrajovou podmínku. Pokud by ji ale neobsahovala, tak by skončila v nekonečné smyčce nebo vyprodukovala nekonečnou datovou strukturu, jako třeba nekonečný seznam. Na nekonečných seznamech je dobré, že je můžeme useknout na jakémkoliv místě. Funkce repeat vezme prvek a vrátí nekonečný seznam, jež obsahuje jenom ten prvek. Dá se to napsat opravdu jednoduše, sledujte.

repeat' :: a -> [a]
repeat' x = x:repeat' x

Zavolání repeat 3 nám vytvoří seznam začínající číslem 3, za kterým následuje nekonečné množství trojek. Takže by se zavolání repeat 3 mohlo vyhodnotit jako 3:repeat 3, což je 3:(3:repeat 3), poté 3:(3:(3:repeat 3)) a tak dále. Výraz repeat 3 nikdy neskončí vyhodnocování, zatímco take 5 (repeat 3) nám vytvoří seznam pěti trojek. To je v podstatě stejné jako replicate 5 3.

Funkce zip vezme dva seznamy a sepne je dohromady. Vyhodnocení zip [1,2,3] [2,3] vrátí [(1,2),(2,3)], protože ořízne delší seznam, aby měl stejnou délku jako ten kratší. Co když sepneme něco s prázdným seznamem? No tak to pak dostaneme prázdný seznam. To je naše okrajová podmínka. Nicméně zip požaduje jako parametr dva seznamy, ve skutečnosti jsou tedy dvě okrajové podmínky.

zip' :: [a] -> [b] -> [(a,b)]
zip' _ [] = []
zip' [] _ = []
zip' (x:xs) (y:ys) = (x,y):zip' xs ys

První dva vzory zadávají, že pokud je první nebo druhý seznam prázdný, dostaneme prázdný seznam. Třetí udává, že se dva sepnuté seznamy rovnají spárování jejich prvních prvků a poté připojení jejich sepnutých zbytků. Při sepnutí seznamů [1,2,3] a ['a','b'] se pokusí sepnout [3] s []. Uplatní se vzor s hraniční podmínkou a takže vznikne výsledek (1,'a'):(2,'b'):[], což je úplně to stejné jako [(1,'a'),(2,'b')].

Napíšeme si ještě jednu další standardní funkci — elem. Ta vezme prvek a seznam a podívá se, jestli se ten prvek vyskytuje v seznamu. Okrajová podmínka, jak to tak u seznamů většinou bývá, je prázdný seznam. Víme, že prázdný seznam neobsahuje žádné prvky, takže zcela určitě nebude obsahovat droidy, které hledáme.

elem' :: (Eq a) => a -> [a] -> Bool
elem' a [] = False
elem' a (x:xs)
    | a == x    = True
    | otherwise = a `elem'` xs

Poměrně jednoduché a očekávatelné. Jestliže není první prvek stejný jako hledaný, zkontrolujeme zbytek. Když narazíme na prázdný seznam, výsledek je False.

Rychle, řaď!

Máme seznam věcí, které mohou být seřazeny. Jejich typ je instancí typové třídy Ord. A teď bychom je chtěli seřadit! Existuje bezvadný řadící algoritmus, nazvaný quicksort. Je to velice chytrý způsob pro řazení věcí. Zatímco je potřeba více než 10 řádků pro napsání quicksortu v imperativních jazycích, implementace v Haskellu je mnohem kratší a elegantnější. Quicksort se stal haskellovou vábničkou. Tudíž si ho tady napíšeme, přestože je psaní quicksortu v Haskellu považováno za celkem podřadné, protože to všichni používají jako ukázku elegance Haskellu.

Takže typové omezení této funkce bude quicksort :: (Ord a) => [a] -> [a]. Žádné překvapení. Okrajová podmínka? Prázdný seznam, což jsme čekali. Seřazený prázdný seznam je prázdný seznam. A teď přichází základní algoritmus: seřazený seznam je seznam, který má všechny hodnoty, jež jsou menší (nebo rovny) prvnímu prvku seznamu, na svém začátku (a tyto hodnoty jsou seřazeny), poté obsahuje první prvek a dále následují všechny hodnoty, které jsou větší než první prvek (jsou také seřazeny). Všimněte si, že jsme v této definici dvakrát zmínili slovo seřazeny, takže pravděpodobně budeme muset udělat rekurzivní volání dvakrát! Také si povšiměte, že jsme to definovali použitím slovesa je pro definici algoritmu, místo abychom řekli udělej tohle, udělej tamto, pak udělej to… V tom spočívá krása funkcionálního programování! Jak zařídíme filtrování seznamu, abychom dostali pouze menší nebo větší prvky než je první prvek z našeho seznamu? Pomocí generátoru seznamu. Takže se do toho pustíme a definujeme si tu funkci.

quicksort :: (Ord a) => [a] -> [a]
quicksort [] = []
quicksort (x:xs) =
    let smallerSorted = quicksort [a | a <- xs, a <= x]
        biggerSorted = quicksort [a | a <- xs, a > x]
    in  smallerSorted ++ [x] ++ biggerSorted

Zkusíme si malý testovací provoz, abychom viděli, zdali to funguje bez chyb.

ghci> quicksort [10,2,5,3,1,6,7,4,2,3,4,8,9]
[1,2,2,3,3,4,4,5,6,7,8,9,10]
ghci> quicksort "prilis zlutoucky kun upel dabelske ody"
"     abcddeeeiikkkllllnoopprsstuuuuyyz"

Hurá! Přesně o tomhle jsem mluvil! Takže když máme, řekněme, [5,1,9,4,6,7,3] a chceme tento seznam seřadit, algoritmus vezme první prvek, což je 5 a poté ho vloží doprostřed dvou seznamů, které jsou menší a větší než ten prvek. Takže v jednom okamžiku máme [1,4,3] ++ [5] ++ [9,6,7]. Víme, že až bude ten seznam celý seřazen, číslo 5 zůstane na čtvrtém místě, protože jsou v seznamu tři čísla menší a tři větší. A teď, jakmile seřadíme [1,4,3] a [9,6,7], dostaneme seřazený seznam! Seřadíme ty dva seznamy použitím stejné funkce. Nakonec se to celé rozpadne tak, že dospějeme k prázdným seznamům a prázdné seznamy jsou už svým způsobem seřazené, vzhledem k tomu, že jsou prázdné. Tady je znázornění:

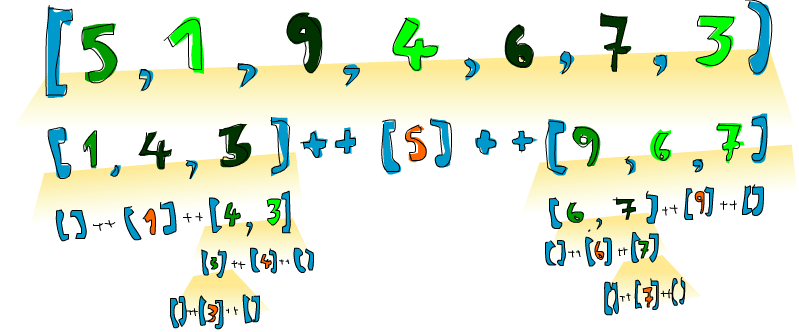
Prvek, který je na svém místě a nebudeme ho posouvat, je znázorněn oranžově. Jestliže je přečtete z leva do prava, uvidíte seřazený seznam. Ačkoliv jsme si vybrali na porovnávání první prvek, mohli jsme si vybrat jakýkoliv jiný. V quicksortu se prvek, který se používá na porovnávání, nazývá pivot. Je vyznačený zeleně. Vybrali jsme si první prvek, protože se jednoduše dá získat pomocí vzoru. Menší prvky než je pivot jsou zvýrazněny světle zeleně a větší prvky než je pivot jsou tmavě zelené. Nažloutlý přechod symbolizuje aplikaci quicksortu.

Myslíme rekurzivně

Udělali jsme toho dosud pomocí rekurze celkem dost a jak jste si zřejmě všimli, je v tom určité schéma. Obvykle si definujeme okrajový případ a poté funkci, která dělá něco s nějakým prvkem a funkcí aplikovanou na zbytek. Nezáleží na tom, jestli to je seznam, strom nebo nějaká jiná datová struktura. Součet je první prvek seznamu plus součet zbytku. Násobek seznamu je první prvek seznamu krát násobek zbytku. Délka seznamu je jednička plus délka zbytku seznamu. A tak dále, a tak dále…

Samozřejmě, tyhle funkce mají rovněž okrajové případy. Okrajový případ je obvykle nějaká možnost, u které aplikace rekurze nedává smysl. Když pracujeme se seznamy, okrajovým případem často bývá prázdný seznam. Jestliže pracujeme se stromy, okrajovým případem obvykle je uzel, jež nemá žádné potomky.

Je to podobné, když rekurzivně pracujete s čísly. Obvykle to má co dělat s nějakým číslem a funkcí aplikovanou na to číslo s úpravou. Ukázali jsme si předtím funkci pro výpočet faktoriálu a to je násobek čísla a faktoriál toho čísla, zmenšeného o jedničku. Tahle aplikace rekurze nedává smysl pro nulu, protože faktoriál je definován pouze pro kladná celá čísla. Často se ukáže, že okrajový případ je identita. Identita pro násobení je jednička, protože jestliže vynásobíte něco jedničkou, dostanete to nazpět. Stejně tak když sčítáme seznamy, definujeme přičtení prázdného seznamu jako nulu, protože nula je identita ve sčítání. U quicksortu je okrajový případ prázdný seznam a identita je také prázdný seznam, protože jestliže připojíme prázdný seznam k seznamu, získame ten stejný seznam.

Takže když se snažíte myslet rekurzivním způsobem při řešení úloh, zkuste přemýšlet nad případy, na které se rekurze nedá aplikovat a podívat se, jestli je můžete použít jako okrajový případ, přemýšlejte o identitách a přemýšlejte o případném rokladu parametrů funkce (například seznamy jsou obvykle rozkládány na první prvek a zbytek pomocí vzorů) a na jakou část použijete rekurzivní volání.