Funkce vyššího řádu

Funkce v Haskellu mohou mít jako parametr jiné funkce a stejně tak mohou být funkce návratovou hodnotou. Funkce, která provádí obě tyhle věci se nazývá funkce vyššího řádu. Funkce vyššího řádu nejsou jenom součástí haskellové praxe, ony jsou v podstatě haskellovou praxí. Ukazuje se, že když chceme zadávat výpočty pomocí definování věcí jaké jsou, místo definování kroků, které změní nějaké stavy a možná pomocí cyklů, funkce vyššího řádu jsou nezbytné. Je to velice silný nástroj na řešení problémů a způsob myšlení o programech.

Curryfikované funkce

Každá funkce v Haskellu bere oficiálně pouze jeden parametr. Tak jak je možné, že jsme si předtím definovali a používali několik funkcí, jež braly více než jeden parametr? No, je to důmyslný trik! Všechny funkce, které předtím akceptovaly několik parametrů, byly curryfikované funkce. Co to znamená? Nejlépe to pochopíte na příkladu. Pojďme vzít naši dobrou známou, funkci max. Vypadá to, že vezme dva parametry a vrátí ten, který je větší. Při vyhodnocování max 4 5 se nejprve vytvoří funkce, která vezme parametr a vrací buď 4 a nebo ten parametr, což závisí na tom, co je větší. Poté je aplikována hodnota 5 na tu funkci a funkce vyprodukuje náš požadovaný výsledek. Zní to jako jazykolam, ale je to ve skutečnosti vážně skvělý koncept. Následující dvě volání jsou ekvivalentní:

ghci> max 4 5
5
ghci> (max 4) 5
5

Poznámka překladatele: pojem curryfikace je pojmenován (stejně jako tento programovací jazyk) podle amerického matematika a logika Haskella Curryho. Protože nebyla ustálena pravopisná podoba slova, lze se setkat i s alternativními verzemi currifikace nebo curryifikace, které označují tu stejnou věc. Curryfikace se zdá být nejsprávnější variantou.

Vložená mezera mezi dvěma věcmi je jednoduše aplikace funkce. Mezera je něco jako operátor a má nejvyšší prioritu. Podívejme se na typ funkce max. Je max :: (Ord a) => a -> a -> a. To může být také zapsáno jako max :: (Ord a) => a -> (a -> a). Což bychom mohli číst: max vezme a a vrátí (to je ta šipka ->) funkci, která vezme nějaké a a vrátí a. To je důvod, proč jsou návratový typ a parametry funkce vždy odděleny pomocí šipek.

A jaký to má pro nás přínos? Jednoduše řečeno, jestliže zavoláme funkci s méně parametry, dostaneme zpátky částečně aplikovanou funkci, což znamená funkci, která požaduje tolik parametrů, kolik jich vynecháme. Použití častečné aplikace (zavolání funkce s méně parametry, jestli chcete) je prima cesta, jak vytvořit za běhu funkce, které můžeme poslat jiné funkci nebo je naplnit nějakými daty.

Podívejte se na tuhle až urážlivě jednoduchou funkci:

multThree :: (Num a) => a -> a -> a -> a
multThree x y z = x * y * z

Co se doopravdy děje, když provedeme multThree 3 5 9 nebo ((multThree 3) 5) 9? Nejprve je aplikován parametr 3 na funkci multThree, protože jsou odděleny mezerou. To vytvoří funkci, která vezme jeden parametr a vrátí funkci. Takže pak se na to aplikuje 5, což vytvoří funkci, která vezme parametr a vynásobí ho 15. Poté se na tu funkci aplikuje 9 a výsledek je 135 nebo tak nějak. Zapamatujte si, že typ této funkce by se dal zapsat jako multThree :: (Num a) => a -> (a -> (a -> a)). Ta věc před první šipkou -> je parametr, který funkce vezme, a ta věc za ní je to co vrací. Takže naše funkce vezme a a vrátí funkci typu (Num a) => a -> (a -> a). Podobně tato funkce vezme a a vrátí funkci typu (Num a) => a -> a. A konečně tato funkce prostě vezme a a vrátí nějaké jiné a. Podívejte se na tohle:

ghci> let multTwoWithNine = multThree 9
ghci> multTwoWithNine 2 3
54
ghci> let multWithEighteen = multTwoWithNine 2
ghci> multWithEighteen 10
180

Zavoláním funkce s méně parametry, abych tak řekl, vytvoříme novou funkci za běhu. Co když chceme vytvořit funkci, která vezme číslo a porovná ho s číslem 100? Mohli bychom to napsat nějak takhle:

compareWithHundred :: (Num a, Ord a) => a -> Ordering
compareWithHundred x = compare 100 x

Jestli že funkci zavoláme s parametrem 99, vrátí GT. Jasná věc. Všimněte si, že x je na vpravo na obou stranách rovnice. A teď přemýšlejte, co vrací výraz compare 100. Vrací funkci, která vezme číslo a porovná ho s číslem 100. Páni! Není to ta funkce, jakou jsme hledali? Můžeme to přepsat jako:

compareWithHundred :: (Num a, Ord a) => a -> Ordering
compareWithHundred = compare 100

Deklarace typu zůstává stejná, portože compare 100 vrací funkci. Porovnání funkce má typ (Ord a) => a -> (a -> Ordering) a zavolání s parametrem 100 vrátí typ (Num a, Ord a) => a -> Ordering. Vkrade se tam další typové omezení, protože číslo 100 je součástí typové třídy Num.

Infixová funkce může být také částečně aplikovaná za použití řezu (sekce). K rozříznutí infixové funkce ji jednoduše obklopíme kulatými závorkami a dodáme parametr na jednu stranu. To vytvoří funkci, která vezme jeden parametr a ten aplikuje na tu stranu, kde chybí operand. Příklad rozříznuté triviální funkce:

divideByTen :: (Floating a) => a -> a
divideByTen = (/10)

Zavolání, řekněme, divideByTen 200 je stejné jako provedení 200 / 10 nebo jako (/10) 200. Funkce, která ověřuj, zda je zadaný znak velké písmeno:

isUpperAlphanum :: Char -> Bool
isUpperAlphanum = (`elem` ['A'..'Z'])

Jedinou neobvyklou věcí u řezu je použití mínusu -. Z definice řezu by (-4) mohl být výsledek z funkce, která vezme číslo a odečte od něj čtyřku. Nicméně, z důvodů pohodlí, (-4) znamená mínus čtyři. Takže když budete chtít vytvořit funkci pro odečítání čtyřky od čísla, jež dostane jako parametr, částečně aplikujte funkci subtract, jako třeba: (subtract 4).

Co se stane, pokud zkusíme zadat do GHCi multThree 3 4, bez toho, abychom výraz definovali pomocí konstrukce let nebo ho předali jiné funkci?

ghci> multThree 3 4
<interactive>:1:0:
    No instance for (Show (t -> t))
      arising from a use of `print' at <interactive>:1:0-12
    Possible fix: add an instance declaration for (Show (t -> t))
    In the expression: print it
    In a 'do' expression: print it

GHCi nám říká, že výraz vyprodukovaný funkcí má typ a -> a, ale neví, jako to vypsat na obrazovku. Funkce nejsou instancí typové třídy Show, takže nemůžeme získat hezkou textovou reprezentaci funkce. Když napíšeme, řekněme, 1 + 1 do příkazové řádky GHCi, nejprve se spočítá výsledek 2 a poté na něj zavolá funkce show, aby se získala textové reprezentace toho čísla. A textová reprezentace čísla 2 je řetězec "2", který je pak vypsán na naši obrazovku.

Trocha vyššího řádu je v pořádku

Funkce mohou mít jako parametry funkce a také vracet funkce. Abychom si to objasnili, vytvoříme si funkci, která vezme další funkci a aplikuje ji na něco dvakrát!

applyTwice :: (a -> a) -> a -> a
applyTwice f x = f (f x)

Jako první si všimněte deklarace typu. Předtím jsme nepotřebovali závorky, protože šipka -> je sama o sobě asociativní zprava. Nicméně tady jsou povinné. Ukazují, že první parametr je funkce, která něco vezme a vrátí tu stejnou věc. Druhým parametrem je něco stejného typu a co má návratovou hodnotu stejného typu. Mohli bychom číst tuhle typovou deklaci curryfikovaným způsobem, ale abychom se vyhnuli bolení hlavy, řekneme prostě, že tahle funkce vezme dva parametry a vrátí jednu věc. Prvním parametrem je nějaká funkce (typu a -> a) a druhý má jako typ to stejné a. První funkce může být třeba Int -> Int nebo String -> String nebo cokoliv jiného. Ale druhý parametr pak musí být stejného typu.

Obsah této funkce je celkem srozumitelný. Prostě vezmeme parametr f jako funkci, aplikujeme na něj x pomocí oddělení mezerou a poté se výsledek aplikuje znovu na funkci f. Kromě toho ještě nějaké blbnutí s funkcemi:

ghci> applyTwice (+3) 10
16
ghci> applyTwice (++ " HAHA") "HEJ"
"HEJ HAHA HAHA"
ghci> applyTwice ("HAHA " ++) "HEJ"
"HAHA HAHA HEJ"
ghci> applyTwice (multThree 2 2) 9
144
ghci> applyTwice (3:) [1]
[3,3,1]

Skvělost a užitečnost částečné aplikace je zjevná. Jestliže naše funkce po nás chce, abychom ji předali funkci, která vezme pouze jeden parametr, můžeme částečně aplikovat funkci na to místo, kde bere ten jeden parametr, a poté ji předat.

A teď využijeme programování s částečnou aplikací na napsání vážně užitečné funkce, která je ve standardní knihovně. Je nazvaná zipWith. Vezme funkci a dva seznamy jako parametr a poté spojí ty dva seznamy aplikací funkce na korespondující elementy. Tady je ukázána naše implementace:

zipWith' :: (a -> b -> c) -> [a] -> [b] -> [c]
zipWith' _ [] _ = []
zipWith' _ _ [] = []
zipWith' f (x:xs) (y:ys) = f x y : zipWith' f xs ys

Podívejte se na typovou deklaraci. První parametr je funkce, která vezme dvě věci a vyprodukuje třetí. Nemusí být stejného typu, ale mohou. Druhý a třetí parametr jsou seznamy. Výsledek je také seznam. První musí být seznam typu a, protože spojovací funkce má první argument typu a. Druhý musí být seznam typu b, protože spojovací funkce má druhý argument také typu b. Výsledek je seznam věcí typu c. Jestliže typová deklarace funkce říká, že akceptuje funkci typu a -> b -> c jako parametr, bude také akceptovat funkci typu a -> a -> a, ale opačně to neplatí! Pamatujte si, že když vytváříme funkce, zvláště ty vyššího řádu, a nejsme si jistí jejich typem, můžeme jednoduše vynechat jejich typovou deklaraci a poté se podívat pomocí příkazu :t na to, co Haskell sám odvodí.

Činnost funkce je celkem podobná normální funkci zip. Okrajové podmínky jsou stejné, akorát je tam navíc jeden argument, spojovací funkce, ale na tom argumentu v okrajových podmínkách nezáleží, takže na to prostě použijeme podtržítko _. A část s posledním vzorem je rovněž podobná funkci zip, jenom nevytváří (x,y), ale f x y. Jedna funkce vyššího řádu může být použita na spoustu odlišných úkolů, pokud je napsána dostatečně obecně. Tady je malá názorná ukázka různých věcí, co naše funkce zipWith' může provádět:

ghci> zipWith' (+) [4,2,5,6] [2,6,2,3]
[6,8,7,9]
ghci> zipWith' max [6,3,2,1] [7,3,1,5]
[7,3,2,5]
ghci> zipWith' (++) ["foo", "bar", "baz"] [" fighters", "man", "mek"]
["foo fighters","barman","bazmek"]
ghci> zipWith' (*) (replicate 5 2) [1..]
[2,4,6,8,10]
ghci> zipWith' (zipWith' (*)) [[1,2,3],[3,5,6],[2,3,4]] [[3,2,2],[3,4,5],[5,4,3]]
[[3,4,6],[9,20,30],[10,12,12]]

Jak můžete vidět, jediná funkce vyššího řádu může být použita k více účelům. Imperativní programování obvykle používá věci jako jsou for smyčky, while smyčky, přiřazení něčeho do proměnné, kontrolování stavu atd. pro dosažení nějakého chování a poté to obalí nějakým rozhraním, třeba funkcí. Funkcionální programování používá funkce vyššího řádu pro abstrahování běžných schémat, jako procházení dvou seznamů po dvojicích a zacházení s těmito dvojicemi nebo dostávání množin řešení a vylučování těch, které nepotřebujeme.

Vytvoříme si další funkci, vyskytující se ve standardní knihovně, nazvanou flip. Flip jednoduše vezme nějakou funkci a vrátí funkci, podobnou naší původní funkci, s tím rozdílem, že jsou první dva argumenty prohozeny. Můžeme ji napsat třeba jako:

flip' :: (a -> b -> c) -> (b -> a -> c)
flip' f = g
    where g x y = f y x

Když si přečteme typovou deklaraci, můžeme říct, že vezme funkci, která požaduje nějaké a a nějaké b a vrátí funkci, která požaduje nějaké b a nějaké a. Druhý pár závorek je opravdu nezbytný, protože funkce jsou implicitně curryfikované a protože je šipka -> asociativní zprava. Typ (a -> b -> c) -> (b -> a -> c) je stejný jako (a -> b -> c) -> (b -> (a -> c)), což je totéž co (a -> b -> c) -> b -> a -> c. Napsali jsme, že g x y = f y x. Pokud to je pravda, pak také platí, že f y x = g x y, ne? Budeme-li to mít na paměti, můžeme funkci definovat dokonce ještě jednodušeji.

flip' :: (a -> b -> c) -> b -> a -> c
flip' f y x = f x y

Tady jsme využili faktu, že jsou funkce curryfikované. Když zavoláme funkci flip' f bez dalších dvou parametrů, vrátí funkci f, která vezme tyhle dva parametry, ale zavolá je v opačném pořadí. Přestože funkce s prohozenými parametry jsou obvykle předány další funkci, můžeme rozmýšlet dopředu a využít curryfikace, když vytváříme funkce vyšších řádů, a napsat, jaký by mohl být jejich konečný výsledek, pokud jsou zavolány s plnou aplikací.

ghci> flip' zip [1,2,3,4] "ahoj"
[('a',1),('h',2),('o',3),('j',4)]
ghci> zipWith (flip' div) [2,2..] [10,8,6,4,2]
[5,4,3,2,1]

Mapy a filtry

map vezme funkci a seznam a aplikuje tu funkci na každý prvek ze seznamu, což vyrobí nový seznam. Podívejme se, jaký má typ a jak je definována.

map :: (a -> b) -> [a] -> [b]
map _ [] = []
map f (x:xs) = f x : map f xs

Z typu zjistíme, že požaduje funkci, která vezme nějaké a a vrátí nějaké b, dále seznam věcí typu a a vrátí seznam věcí typu b. Je zajímavé, jak pouhým pohledem na typ funkce můžete občas říct, co funkce dělá. Funkce map je jedna z těch opravdu všestranných funkcí vyššího řádu, které mohou být použity na milión způsobů. Tady je v akci:

ghci> map (+3) [1,5,3,1,6]
[4,8,6,4,9]
ghci> map (++ "!") ["BUM", "BÁC", "PRÁSK"]
["BUM!","BÁC!","PRÁSK!"]
ghci> map (replicate 3) [3..6]
[[3,3,3],[4,4,4],[5,5,5],[6,6,6]]
ghci> map (map (^2)) [[1,2],[3,4,5,6],[7,8]]
[[1,4],[9,16,25,36],[49,64]]
ghci> map fst [(1,2),(3,5),(6,3),(2,6),(2,5)]
[1,3,6,2,2]

Pravděpodobně jste si všimli, že by se všechny ty ukázky daly přepsat pomocí generátorů seznamu. Když napíšeme map (+3) [1,5,3,1,6], tak to je stejné jako [x+3 | x <- [1,5,3,1,6]]. Nicméně použití funkce map je mnohem čitelnější pro případy, ve kterých pouze aplikujete nějakou funkci na prvek ze seznamu, zvláště pokud se vypořádáváte s mapováním mapování a pak by celá ta věc s hromadou závorek byla dost komplikovaná.

filter je funkce, která vezme predikát (predikát je funkce, která nám řekne, jestli je něco pravda nebo nepravda, takže v našem případě to je funkce vracející booleovskou hodnotu) a nějaký seznam a potom vrátí seznam prvků, které vyhovují predikátu. Typ a implementace vypadají nějak takhle:

filter :: (a -> Bool) -> [a] -> [a]
filter _ [] = []
filter p (x:xs)
    | p x       = x : filter p xs
    | otherwise = filter p xs

Celkem jednoduchá věc. Jestliže se p x vyhodnotí jako True, prvek se zařadí do nového seznamu. Pokud ne, zahodí ho. Nějaké ukázky použití:

ghci> filter (>3) [1,5,3,2,1,6,4,3,2,1]
[5,6,4]
ghci> filter (==3) [1,2,3,4,5]
[3]
ghci> filter even [1..10]
[2,4,6,8,10]
ghci> let notNull x = not (null x) in filter notNull [[1,2,3],[],[3,4,5],[2,2],[],[],[]]
[[1,2,3],[3,4,5],[2,2]]
ghci> filter (`elem` ['a'..'z']) "SmĚjeŠ sE mI, pRoToŽe jSeM JinÝ."
"mjesmpooejein"
ghci> filter (`elem` ['A'..'Z']) "SmějU se váM, prOTožE jSte sTejní."
"SUMOTEST"

Tohle všechno by také dalo docílit pomocí generátorů seznamu s predikáty. Neexistuje žádná sada pravidel, kdy použít map a filter versus generátor seznamu, musíte se prostě v závislosti na kódu a kontextu rozhodnout, co je více čitelné. K aplikaci několika predikátů ve funkci filter je u generátoru seznamu ekvivalentní buď několikanásobné filtrování nebo spojení predikátů pomocí logické funkce &&.

Vzpomínáte si na naši funkci quicksort z předchozí kapitoly? Použili jsme generátor seznamu na odfiltrování prvků seznamu, které byly menší (nebo rovné) a větší než pivot. Můžeme docílit stejné funkčnosti a ještě lepší čitelnosti použitím funkce filter:

quicksort :: (Ord a) => [a] -> [a]
quicksort [] = []
quicksort (x:xs) =
    let smallerSorted = quicksort (filter (<=x) xs)
        biggerSorted = quicksort (filter (>x) xs)
    in  smallerSorted ++ [x] ++ biggerSorted

Mapování a filtrování jsou živobytím nářadí funkcionálního programátora. Hm. Nezáleží na tom, jestli budete využívat spíše funkce map a filter oproti generátoru seznamu. Vzpomeňte si, jak jsme řešili problém hledání pravoúhlých trojúhelníků s určitým obvodem. V imperativním programování bychom to mohli vyřešit zanořením tří smyček a následným testováním, jestli aktuální kombinace dá dohromady pravoúhlý trojúhelník a jestli má správný obvod. Pokud by to byl ten případ, mohli bychom to vytisknout na obrazovku nebo něco. Ve funkcionálním programování se tohoto schématu dá docílit mapováním a filtrováním. Vytvoříte si funkci, která vezme nějakou hodnotu a vyprodukuje nějaký výsledek. Namapujeme tuhle funkci na seznam hodnot a poté z něj odfiltrujeme vyhovující výsledky. I když něco namapujeme na seznam vícekrát a poté to několikrát odfiltrujeme projde to díky lenosti Haskellu tím seznamem pouze jednou.

Pojďme najít největší číslo pod 100000, které je dělitelné číslem 3829. Abychom toho docílili, jednoduše odfiltrujeme množinu možností, o kterých víme, že se mezi nimi nalézá řešení.

largestDivisible :: (Integral a) => a
largestDivisible = head (filter p [100000,99999..])
    where p x = x `mod` 3829 == 0

Nejprve si vytvoříme seznam všech čísel menší než 100000, sestupně. Poté ho odfiltrujeme naším predikátem a protože jsou čísla seřazena sestupně, největší číslo, které vyhovuje našemu predikátu, bude prvním prvkem našeho seznamu. Jako výchozí množinu jsme dokonce nemuseli použít konečný seznam. Opět je tu vidět lenost v akci. Protože jsme nakonec využili pouze první prvek z filtrovaného seznamu, nezáleží na tom, jestli je ten seznam konečný nebo ne. Vyhodnocování se zastaví, když se nalezne první přijatelné řešení.

Dále zkusíme najít součet všech lichých čtverců, které jsou menší než 10000. Nejprve si ale představíme funkci takeWhile, protože ji využijeme v našem řešení. Vezme nějaký predikát a seznam a poté ten seznam prochází od začátku a vrací jeho prvky, dokud vyhovují predikátu. Jakmile se narazí na prvek, pro který predikát neplatí, procházení se zastaví. Pokud bychom chtěli získat první slovo z řetězce "sloni si umí užívat", mohli bychom udělat něco jako takeWhile (/= ' ') "sloni si umí užívat" a to by nám vrátilo řetězec "sloni". Dobře. Součet všech lichých čtverců, které jsou menší než 10000. Začneme namapováním funkce (^2) na nekonečný seznam [1..]. Poté to odfiltrujeme, abychom dostali jen ty liché. A pak, vybereme prvky, které jsou menší než 10000. A nakonec to celé sečteme. Nemusíme si na to ani definovat funkci, můžeme to vyřešit jedním řádkem v GHCi:

ghci> sum (takeWhile (<10000) (filter odd (map (^2) [1..])))
166650

Skvělé! Začali jsme s nějakými počátečními daty (nekonečný seznam všech přirozených čísel) a poté jsme na něj namapovali funkci, odfiltrovali ho a zredukovali na část, která vyhovovala naším potřebám, a tu jsme prostě sečetli. Mohli jsme to také zapsat pomocí generátoru seznamu:

ghci> sum (takeWhile (<10000) [m | m <- [n^2 | n <- [1..]], odd m])
166650

Je to otázka vkusu, který zápis se vám bude líbit více. Znovu, tohle celé umožňuje lenost v Haskellu. Můžeme namapovat a odfiltrovat nekonečný seznam, protože se to nebude ve skutečnosti mapovat a filtrovat hned, tyhle akce se odloží. Jenom když donutíme Haskell ukázat nám součet, funkce sum řekne funkci takeWhile, že potřebuje čísla. Funkce takeWhile přinutí filtry a mapy, aby se prováděly, ale jenom dokud nepotká číslo větší nebo rovné 10000.

V našem dalším problému se budeme vypořádávat s Collatzovou řadou. Vezmeme nějaké přirozené číslo. Jestliže je to číslo sudé, vydělíme ho dvěma. Jestliže je liché, vynásobíme ho třemi a přičteme k tomu jedničku. Na výsledné číslo aplikujeme stejný postup, což vyprodukuje nové číslo a tak dále. V podstatě dostaneme posloupnost čísel. Má se za to, že pro libovolné počáteční číslo skončí posloupnost jedničkou. Takže pokud vezmeme jako počáteční číslo 13, dostaneme tuhle řadu: 13, 40, 20, 10, 5, 16, 8, 4, 2, 1. Výraz 13 * 3 + 1 se rovná 40. Číslo 40 vydělené 2 je 20, atd. Vidíme, že tato posloupnost má deset členů.

A teď chceme znát odpověď na tohle: pro všechna čísla mezi 1 a 100, kolik posloupností je delších než 15? Nejprve si napíšeme funkci, která vytvoří posloupnost:

chain :: (Integral a) => a -> [a]
chain 1 = [1]
chain n
    | even n =  n:chain (n `div` 2)
    | odd n  =  n:chain (n*3 + 1)

Protože posloupnost končí jedničkou, je to okrajový případ. To je celkem standardní rekurzivní funkce.

ghci> chain 10
[10,5,16,8,4,2,1]
ghci> chain 1
[1]
ghci> chain 30
[30,15,46,23,70,35,106,53,160,80,40,20,10,5,16,8,4,2,1]

Jej! Vypadá to, že funguje korektně. A nyní přichází funkce, jež nám poskytne odpověď na naši otázku:

numLongChains :: Int
numLongChains = length (filter isLong (map chain [1..100]))
    where isLong xs = length xs > 15

Namapujeme funkci chain na seznam [1..100], abychom dostali seznam posloupností, které jsou znázorněny seznamem. Poté je odfiltrujeme pomocí predikátu, který se jednoduše podívá, jestli má seznam více než 15 prvků. Jakmile jsme hotoví s filtrováním, podíváme se, kolik posloupností zbylo ve výsledném seznamu.

Použitím funkce map můžeme také vytvořit věci jako map (*) [0..], minimálně z toho důvodu, abychom si ukázali, jak funguje curryfikace a že jsou (částečně aplikované) funkce opravdové hodnoty, které můžete posílat dalším funkcím nebo vkládat do seznamů (jenom je nemůžete změnit na řetězce). Zatím jsme pouze mapovali funkce, které použily jeden parametr na celý seznam, jako třeba map (*2) [0..], abychom obdrželi seznam typu (Num a) => [a], ale můžeme také bez problémů používat map (*) [0..]. Stane se zde to, že je číslo v seznamu aplikováno na funkci *, která má typ (Num a) => a -> a -> a. Aplikace pouze jednoho parametru na funkci, která vezme dva parametry, vrátí funkci, která požaduje jeden parametr. Jestliže ji namapujeme * na seznam [0..], vrátí se nám seznam funkcí, které požadují pouze jeden parametr, takže je to typ (Num a) => [a -> a]. Když napíšeme map (*) [0..], vytvoří to stejný seznam jako kdybychom napsali [(*0),(*1),(*2),(*3),(*4),(*5)…].

ghci> let listOfFuns = map (*) [0..]
ghci> (listOfFuns !! 4) 5
20

Získání prvku s indexem 4 z našeho seznamu vrátí funkci, která odpovídá (*4). A poté jednoduše aplikujeme číslo 5 na tu funkci. Takže je to stejné jako napsání (* 4) 5 nebo prostě 5 * 4.

Lambdy

Lambdy jsou v zásadě anonymní funkce, které jsou používané, protože často potřebujeme nějakou funkci jenom jednou. Obvykle si vytváříme lambdu, abychom ji předali funkci vyššího řádu. Pro vytvoření lambdy napíšeme znak \ (protože vypadá jako řecké písmeno lambda, když na něj pořádně zamžouráte) a poté napíšeme parametry, oddělené mezerami. Za tím následuje šipka -> a tělo funkce. Obvykle to celé obklopíme kulatými závorkami, protože jinak to sahá dál napravo.

Jestliže se podíváte o pětadvacet centimetrů nahoru, uvidíte, že jsme v naší funkci numLongChains použili konstrukci where, abychom si vytvořili funkci isLong, kterou jsme předali funkci filter. Takže místo toho můžeme použít lambdu:

numLongChains :: Int
numLongChains = length (filter (\xs -> length xs > 15) (map chain [1..100]))

Lambdy jsou výrazy, to je důvod, proč je můžeme jen tak předat. Výraz (\xs -> length xs > 15) vrátí funkci, která nám poví, jaké seznamy jsou delší než 15.

Lidé, jež nejsou důkladně obeznámeni s tím, jak curryfikace a částečná aplikace funguje, často používají lambdy tam, kde nemusí být. Kupříkladu výrazy map (+3) [1,6,3,2] a map (\x -> x + 3) [1,6,3,2] jsou ekvivalentní, protože (+3) a (\x -> x + 3) jsou obě funkce, co vezmou nějaké číslo a přičtou k němu trojku. Netřeba dodávat, že v tomhle případě je používat lambdu hloupé, jelikož je částečná aplikace mnohem čitelnější.

Lambdy mohou mít, stejně jako běžné funkce, libovolný počet parametrů:

ghci> zipWith (\a b -> (a * 30 + 3) / b) [5,4,3,2,1] [1,2,3,4,5]
[153.0,61.5,31.0,15.75,6.6]

A můžete také, stejně jako v běžných funkcích, používat vzory. Jediný rozdíl je v tom, že nemůžete definovat více vzorů pro jeden parametr, jako napsání [] a (x:xs) na místo stejného parametru a poté ověřovat aktuální hodnotu. Jestliže vzory selžou u lambdy, dojde k běhové chybě, takže opatrně se vzory v lambda funkcích!

ghci> map (\(a,b) -> a + b) [(1,2),(3,5),(6,3),(2,6),(2,5)]
[3,8,9,8,7]

Lambdy se normálně obklopují kulatými závorkami, pokud nechceme, aby sahaly dál napravo. Je to zajímavé: díky směru, v jakém jsou funkce automaticky curryfikované, jsou tyhle dva zápisy ekvivalentní:

addThree :: (Num a) => a -> a -> a -> a
addThree x y z = x + y + z

addThree :: (Num a) => a -> a -> a -> a
addThree = \x -> \y -> \z -> x + y + z

Jestliže definujeme takovou funkci, je zřejmé, proč má takovou typovou deklaraci, jako má. U typové deklarace i rovnice jsou tři šipky ->. Samozřejmě, první způsob zápisu funkcí je mnohem čitelnější, druhý je spíše fígl na ukázání curryfikace.

Nicméně existují případy, ve který je použití této notace skvělé. Myslím si, že funkce flip je nejvíce přehledná, když je zapsaná nějak takhle:

flip' :: (a -> b -> c) -> b -> a -> c
flip' f = \x y -> f y x

Ačkoliv to je stejné, jako když napíšeme flip' f x y = f y x, ozřejmíme tím, že to bude většinou použito pro vytvoření nové funkce. Nejobvyklejší použití funkce flip je zavolat ji pouze s jedním parametrem a předat výslednou funkci pomocí mapy nebo filtru. Takže používejte lambda funkce tímhle způsobem, když chcete zdůraznit, že je vaše funkce určená pro částečnou aplikaci a pro předání jiné funkci jako parametr.

Akumulační funkce fold

Když jsme se předtím zabývali rekurzí, všímali jsme si schématu u mnoha rekurzivních funkcí, které zacházejí se seznamy. Obvykle jsme měli okrajový případ pro prázdný seznam. Představili jsme si vzor x:xs a poté jsme prováděli určité akce týkající se prvku a zbytku seznamu. Ukázalo se, že to je velmi častý vzor, takže bylo zavedeno pár užitečných funkcí, které ho zapouzdřují. Těmto funkcím se říká foldy (skládače). Jsou podobné funkci map, akorát omezují seznam na nějakou jednu hodnotu.

Fold vezme binární funkci, nějakou počáteční hodnotu (rád ji říkám akumulátor) a seznam na poskládání. Binární funkce sama o sobě požaduje dva parametry. Je zavolána s akumulátorem a prvním (nebo posledním) prvkem a vytvoří nový akumulátor. Poté je tato binární funkce zavolána s novým akumulátorem a s novým prvním (nebo posledním) prvkem a tak dále. Jakmile projdeme celý seznam, zbyde nám pouze akumulátor, na který jsme seznam zredukovali.

Nejprve se podívejme na funkci foldl, také nazvaná levý fold. Poskládá seznam z levé strany. Binární funkce je aplikována na počáteční hodnotu a první prvek ze seznamu. To vytvoří novou akumulační hodnotu a binární funkce je zavolána s tou hodnotou a dalším prvkem atd.

Pojďme si znovu implementovat funkci sum, jenom tentokrát použijeme fold místo explicitní rekurze.

sum' :: (Num a) => [a] -> a
sum' xs = foldl (\acc x -> acc + x) 0 xs

Zkouška, raz, dva, tři:

ghci> sum' [3,5,2,1]
11

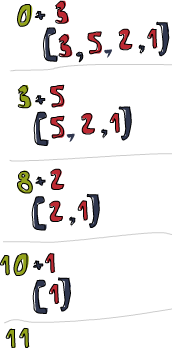
Podíváme se do hloubky, co se při tomto vyhodnocování děje. Funkce \acc x -> acc + x je binární. Počáteční hodnota je tu 0 a xs je seznam, který bude poskládán. Na začátku je dosazeno číslo 0 na místo parametru acc v binární funkci a číslo 3 je (jako současný prvek) dosazeno na místo parametru x. Sečtení 0 + 3 vytvoří číslo 3 a to se stane novou akumulační hodnotou, dá-li se to tak říct. Dále je použité číslo 3 jako akumulační hodnota a číslo 5 jako aktuální prvek a tím pádem se číslo 8 stane novým akumulátorem. Pokračujeme, máme parametry 8 a 2, nová akumulační hodnota je tedy 10. A nakonec je použito číslo 10 jako akumulační hodnota a číslo 1 jako aktuální prvek, což vytvoří číslo 11. Gratuluji, zvládli jsme skládání!

Tento odborný nákres nalevo objasňuje, co se ve foldu odehrává, krok za krokem (den za dnem!). Zelenohnědé číslo je akumulační hodnota. Můžete vidět, jak je seznam takříkajíc požírán zleva akumulátorem. Mňamy, mňam, mňam! Jestliže vezmeme v úvahu, že funkce mohou být curryfikované, můžeme zapsat tuhle funkci ještě více stručněji, jako třeba:

sum' :: (Num a) => [a] -> a
sum' = foldl (+) 0

Lambda funkce (\acc x -> acc + x) dělá to stejné co (+). Můžeme vynechat xs jako parametr, protože zavolání foldl (+) 0 vrátí funkci, která vezme seznam. Obecně, jestliže máte funkci jako foo a = bar b a, můžete ji díky curryfikaci přepsat jako foo = bar b.

Rozhodopádně si pojďme napsat vlastní funkci s levým foldem, než pokročíme k pravému. Jsem si jistý, že všichni víte, že funkce elem kontroluje, jestli se určitá hodnota vyskytuje v seznamu, takže to nebudu opakovat (jejda, zrovna jsem to udělal!). Pojďme si ji napsat pomocí levého foldu.

elem' :: (Eq a) => a -> [a] -> Bool
elem' y ys = foldl (\acc x -> if x == y then True else acc) False ys

Fajn, fajn, fajn, co to tady máme? Počáteční hodnota — a zároveň akumulátor — je zde booleovská hodnota. Typ akumulační hodnoty a typ výsledku je vždycky stejný, když se zabýváme s foldy. Pamatujte si, že pokud vůbec nevíte, co použít za počáteční hodnotu, dá vám určitou představu. Začneme s False. Dává to smysl použít False jako počáteční hodnotu. Předpokládáme, že tam ta hodnota není. Také když zavoláme fold na prázdný seznam, výsledkem bude počáteční hodnota. Pak zkontrolujeme, jestli se aktuální prvek rovná tomu, který hledáme. Jestliže je, nastavíme akumulátor na True. Jestliže není, jednoduše necháme akumulátor nezměněný. Pokud byl předtím False, zůstane stejný, protože se prvky nerovnají. Pokud byl True, necháme ho tak.

Pravý fold, foldr, pracuje podobně jako levý, jenom s tím rozdílem, že akumulátor požírá hodnoty zprava. Také binární funkce pro levý fold má akumulátor jako první parametr a aktuální hodnotu jako druhý (tedy \acc x -> …), binární funkce pro pravý fold má aktuální hodnotu jako první parametr a akumulátor jako druhý (tedy \x acc -> …). Dává to celkem smysl, že pravý fold má akumulátor napravo, protože skládá z pravé strany.

Hodnota akumulátoru (a tudíž i výsledek) ve foldu může být jakéhokoliv typu. Může to být číslo, booleovská proměnná nebo i seznam. Implementujeme si funkci map pomocí pravého foldu. Akumulátor bude seznam, budeme akumulovat mapovaný seznam prvek po prvku. Z toho je jasné, že počáteční prvek bude prázdný seznam.

map' :: (a -> b) -> [a] -> [b]
map' f xs = foldr (\x acc -> f x : acc) [] xs

Jestliže namapujeme funkci (+3) na seznam [1,2,3], přistoupíme k seznamu z pravé strany. Vezmeme poslední prvek, což je číslo 3, a aplikujeme na něj funkci, z čehož se stane číslo 6. Poté ho připojíme k akumulátoru, což nám dává []. Výraz 6:[] je [6] a to je současný akumulátor. Aplikujeme (+3) na číslo 2, což je 5, které připojíme (:) k akumulátoru, takže je akumulátor teď [5,6]. Aplikujeme (+3) na číslo 1 a to připojíme k akumulátoru, takže je konečná hodnota [4,5,6].

Samozřejmě bychom si mohli napsat tuhle funkci pomocí levého foldu. Bylo by to map' f xs = foldl (\acc x -> acc ++ [f x]) [] xs, ale problém je v tom, že funkce ++ mnohem náročnější než :, takže obvykle používáme pravé foldy na sestavování nových seznamů ze seznamu.

Když obrátíte seznam, můžete na něj použít pravý fold místo levého a naopak. Někdy ho ani nemusíte obracet. Funkce sum může být implementována prakticky stejně pomocí levého a pravého foldu. Hlavní rozdíl je v tom, že pravý fold může pracovat s nekonečnými seznamy, kdežto levý ne! Pro objasnění, pokud někdy vezmete nekonečný seznam od určitého místa a začnete ho skládat zprava, dostanete se časem na začátek toho seznamu. Nicméně pokud vezmete nekonečný seznam od určitého místa a zkusíte ho skládat zleva, nikdy se nedostanete na konec!

Foldy mohou být použity pro zápis funkcí, u kterých procházíme seznam jedenkrát, prvek po prvku, a poté vrátíme něco, co je na tom průchodu založené. Kdykoliv hodláte projít seznam, abyste něco vrátili, je pravděpodobné, že chcete fold. To je důvod, proč jsou foldy, spolu s mapami a filtry, jeden z nejužitečnějších typů funkcí ve funkcionálním programování.

Funkce foldl1 a foldr1 fungují podobně jako foldl a foldr, jenom jim nemusíte explicitně poskytnout počáteční hodnotu. Předpokládá se, že první (nebo poslední) prvek ze seznamu bude počáteční hodnota a ta se poté začne skládat s následujícími hodnotami. Budeme-li to mít na mysli, můžeme funkci sum napsat jako sum = foldl1 (+). Protože záleží na tom, aby skládaný seznam obsahoval alespoň jeden prvek, vyhodí se běhová chyba, jestliže tyto funkce zavoláme na prázdný seznam. Na druhou stranu, funkce foldl and foldr fungují i s prázdnými seznamy. Když pracujete s foldy, popřemýšlejte o tom, jak by se měly chovat na prázdných seznamech. Jestliže nedává smysl pracovat s prázdným seznamem, můžete spíše použít funkci foldl1 nebo foldr1.

Abych vám ukázal, jak jsou foldy užitečné, naprogramujeme si pár standardních funkcí za pomocí foldů:

maximum' :: (Ord a) => [a] -> a
maximum' = foldr1 (\x acc -> if x > acc then x else acc)

reverse' :: [a] -> [a]
reverse' = foldl (\acc x -> x : acc) []

product' :: (Num a) => [a] -> a
product' = foldr1 (*)

filter' :: (a -> Bool) -> [a] -> [a]
filter' p = foldr (\x acc -> if p x then x : acc else acc) []

head' :: [a] -> a
head' = foldr1 (\x _ -> x)

last' :: [a] -> a
last' = foldl1 (\_ x -> x)

Funkci head je lepší napsat pomocí vzorů, ale takhle je ukázaný zapis pomocí foldů. Řekl bych, že naše definice funkce reverse' je celkem důmyslná. Vezmeme jako počáteční hodnotu prázdný seznam a poté postupujeme v našem seznamu zleva a připojujeme prvky k akumulátoru. Nakonec si vytvoříme obrácený seznam. Binární funkce \acc x -> x : acc vypadá podobně jako funkce :, jenom má přehozené parametry. To je důvod, proč bychom mohli zapsat naši funkci na obracení seznamu jako foldl (flip (:)) [].

Další způsob, jak si představit pravé a levé foldy je takový: řekněme, že máme pravý fold, binární funkce je f a počáteční funkce je z. Jestliže skládáme zprava seznam [3,4,5,6], děláme v podstatě tohle: f 3 (f 4 (f 5 (f 6 z))). Funkce f je zavolána na poslední prvek v seznamu a akumulátor, výsledná hodnota je předána jako akumulátor další hodnotě a tak dále. Jestliže funkce f bude + a počáteční akumulátor 0, celý výraz bude 3 + (4 + (5 + (6 + 0))), což dává výsledek 18. Nebo když napíšeme + jako prefixovou funkci, bude z toho (+) 3 ((+) 4 ((+) 5 ((+) 6 0))). Podobně, když skládáme zleva ten stejný seznam pomocí binární funkce g a akumulátorem z, vznikne nám výraz g (g (g (g z 3) 4) 5) 6. Jestliže použijeme jako binární funkci flip (:) a jako akumulátor [] (takže obracíme seznam), dostaneme z toho flip (:) (flip (:) (flip (:) (flip (:) [] 3) 4) 5) 6. A samozřejmě, když vyhodnotíte tenhle výraz, dostanete seznam [6,5,4,3].

Funkce scanl a scanr jsou stejné jako foldl a foldr, jenom vypisují všechny dílčí stavy akumulátoru ve formě seznamu. Existují také funkce scanl1 a scanr1, jež jsou analogické k funkcím foldl1 a foldr1.

ghci> scanl (+) 0 [3,5,2,1]
[0,3,8,10,11]
ghci> scanr (+) 0 [3,5,2,1]
[11,8,3,1,0]
ghci> scanl1 (\acc x -> if x > acc then x else acc) [3,4,5,3,7,9,2,1]
[3,4,5,5,7,9,9,9]
ghci> scanl (flip (:)) [] [3,2,1]
[[],[3],[2,3],[1,2,3]]

Když používáte funkci scanl, konečný výsledek bude poslední prvek z výsledného seznamu, kdežto scanr umístí výsledek na začátek.

Scany se používají na monitorování postupu funkce, která může být napsána pomocí foldu. Odpovězme si na otázku: „Kolik prvků je potřeba pro součet druhých odmocnin všech přirozených čísel, aby přesáhl hodnotu 1000?“ Abychom dostali odmocniny všech přirozených čísel, stačí napsat jenom map sqrt [1..]. A teď, pro získání součtu bychom mohli použít fold, ale protože nás zajímá, jak součet postupuje, použijeme scan. Jakmile jsme hotoví se scanem, podíváme se, kolik součtů je pod 1000. První součet v seznamu scanů bude normálně jednička. Druhý bude jedna plus druhá odmocnina ze dvou. Třetí bude to předtím plus druhá odmocnina ze tří. Jestliže existuje X součtů menších než 1000, bude potřeba X + 1 prvků pro součet, přesahující 1000.

sqrtSums :: Int
sqrtSums = length (takeWhile (<1000) (scanl1 (+) (map sqrt [1..]))) + 1

ghci> sqrtSums
131
ghci> sum (map sqrt [1..131])
1005.0942035344083
ghci> sum (map sqrt [1..130])
993.6486803921487

Použijeme zde funkci takeWhile místo filter, protože funkce filter neumí pracovat s nekonečnými seznamy. I když víme, že je seznam vzrůstající, filter to neví, takže použijeme takeWhile, abychom generování seznamu scanů přerušili při prvním výskytu součtu větším než 1000.

Aplikace funkce pomocí $

Dále se podíváme na funkci $, která se také nazývá aplikace funkce. Nejprve se mrkneme, jak je definována:

($) :: (a -> b) -> a -> b
f $ x = f x

Co to sakra je? Co je tohle za neužitečný operátor? Je to jenom aplikovaná funkce! No skoro, ale nejen to! Zatímco obyčejná aplikace funkce (vložení mezery mezi dvě věci) má celkem vysokou prioritu, funkce $ má prioritu nejnižší. Aplikace funkce pomocí mezery je asociativní zleva (takže f a b c je to stejné co ((f a) b) c)), aplikace funkce pomocí $ je asociativní zprava.

To je sice skvělé, ale jak nám tohle pomůže? Většinou ji využijeme pro konvenci, abychom nemuseli psát tolik závorek. Předpokládejme výraz sum (map sqrt [1..130]). Protože má funkce $ tak nízkou prioritu, můžeme ho přepsat na sum $ map sqrt [1..130], čímž jsme si ušetřili drahocenné úhozy na klávesnici! Když se narazí na operátor $, výraz napravo je aplikován jako parametr funkci nalevo. A co takhle sqrt 3 + 4 + 9? Tenhle výraz sečte devítku, čtyřku a druhou odmocninu trojky. Kdybychom chtěli druhou odmocninu z 3 + 4 + 9, museli bychom napsat sqrt (3 + 4 + 9) nebo s použitím operátoru $ můžeme napsat sqrt $ 3 + 4 + 9, protože operátor $ má nižší prioritu než všechny ostatní. To je důvod, proč si můžete představit funkci $ jako obdobu toho, když napíšeme otevírací závorku a poté někam hodně daleko na pravou stranu výrazu závorku uzavírací.

A co třeba sum (filter (> 10) (map (*2) [2..10]))? No protože je operátor $ asociativní zprava, výraz f (g (z x)) odpovídá výrazu f $ g $ z x. A tak můžeme přepsat sum (filter (> 10) (map (*2) [2..10])) na sum $ filter (> 10) $ map (*2) [2..10].

Kromě zbavování se závorek nám operátor $ umožňuje zacházet s aplikací funkce jako s jinými funkcemi. Tímto způsobem můžeme kupříkladu namapovat aplikaci funkce na seznam funkcí.

ghci> map ($ 3) [(4+), (10*), (^2), sqrt]
[7.0,30.0,9.0,1.7320508075688772]

Skládání funkcí

V matematice je skládání funkcí (kompozice) definováno takto: 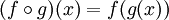, což znamená, že skládání dvou funkcí vytvoří novou funkci, kterou když zavoláme s parametrem, řekněme x, je ekvivalentní zavolání funkce g s parametrem x a poté zavolání funkce f na výsledek.

V Haskellu je skládání funkcí v podstatě stejná věc. Pro skládání funkcí používáme funkci ., jež je definována následovně:

(.) :: (b -> c) -> (a -> b) -> a -> c
f . g = \x -> f (g x)

Popřemýšlejte nad typovou deklarací. Funkce f musí mít jako parametr hodnotu se stejným typem jako je typ návratové hodnoty g. Takže výsledná funkce vezme parametr stejného typu jako požaduje g a vrátí hodnotu shodného typu, jako vrací f. Výraz negate . (* 3) vrací funkci, která vezme nějaké číslo, vynásobí ho trojkou a poté zneguje.

Jedno z použití skládání funkcí je vytvoření funkcí za chodu pro předání jiným funkcím. Jasně, můžeme na to použít lambdu, ale častokrát je skládání funkcí čistější a stručnější. Řekněme, že máme seznam čísel a chceme je všechny převést na záporná čísla. Jeden ze způsobů, jak to provést, by mohl být negace absolutní hodnoty, jako tady:

ghci> map (\x -> negate (abs x)) [5,-3,-6,7,-3,2,-19,24]
[-5,-3,-6,-7,-3,-2,-19,-24]

Všimněte si lambdy, že vypadá jako výsledek skládání funkcí. S využitím skládání funkcí to můžeme přepsat na:

ghci> map (negate . abs) [5,-3,-6,7,-3,2,-19,24]
[-5,-3,-6,-7,-3,-2,-19,-24]

Báječné! Skládání funkcí je asociativní zprava, takže můžeme skládat více funkcí najednou. Výraz f (g (z x)) je stejný jako (f . g . z) x. Pokud tohle vezmeme v úvahu, můžeme převést výraz:

ghci> map (\xs -> negate (sum (tail xs))) [[1..5],[3..6],[1..7]]
[-14,-15,-27]

na výraz:

ghci> map (negate . sum . tail) [[1..5],[3..6],[1..7]]
[-14,-15,-27]

Ale co funkce s více parametry? Když je chceme použít při skládání funkcí, obvykle je musíme částečně aplikovat natolik, abychom dostali funkci, která bere pouze jeden parametr. Například sum (replicate 5 (max 6.7 8.9)) může být zapsáno jako (sum . replicate 5 . max 6.7) 8.9 nebo jako sum . replicate 5 . max 6.7 $ 8.9. O co tady jde je tohle: je vytvořena funkce, která vezme max 6.7 a aplikuje na to replicate 5. Poté se vytvoří funkce, co vezme předchozí výsledek a provede součet. A nakonec je tato funkce zavolána na číslo 8.9. Ale obvykle to čteme takto: číslo 8.9 se aplikuje na výraz max 6.7, poté se na to aplikuje výraz replicate 5 a nakonec se na to aplikuje funkce sum. Jestliže chcete zapsat výraz s hromadou závorek za pomocí skládání funkcí, můžete začít vložením posledního parametru nejvnitřnější funkce za operátor $ a poté prostě skládat všechny ostatní volání funkcí, zapsat je bez jejich posledního parametru a vkládat mezi ně tečky. Pokud máte výraz replicate 100 (product (map (*3) (zipWith max [1,2,3,4,5] [4,5,6,7,8]))), můžete ho zapsat jako replicate 100 . product . map (*3) . zipWith max [1,2,3,4,5] $ [4,5,6,7,8]. Jestliže výraz končí třemi kulatými závorkami, je pravděpodobné, že po předělání na skládání funkcí bude obsahovat tři operátory skládání.

Další obvyklé použití skládání funkcí je definování funkce v takzvaném pointfree stylu (také se mu říká pointless styl). Vezmeme si pro příklad funkci, kterou jsme si napsali dříve:

sum' :: (Num a) => [a] -> a
sum' xs = foldl (+) 0 xs

Část xs je přítomna na obou pravých stranách. Díky curryfikaci můžeme xs vynechat, protože zavolání foldl (+) 0 vytvoří funkci, která požaduje seznam. Zápisu sum' = foldl (+) 0 takové funkce se říká zápis v pointfree stylu. Jak bychom mohli napsat tohle v pointfree stylu?

fn x = ceiling (negate (tan (cos (max 50 x))))

Nemůžeme se jednoduše zbavit x na obou stranách. Parametr x je v těle funkce uzávorkovaný. Výraz cos (max 50) by nedával smysl. Nemůžete dostat kosinus funkce. Uděláme to, že vyjádříme fn jako skládání funkcí.

fn = ceiling . negate . tan . cos . max 50

Skvělé! Pointfree styl bývá často čitelnější a stručnější, protože nás nutí přemýšlet o funkcích a o výsledcích skládání funkcí místo přemýšlení nad daty a jejich přesouvání. Můžete vzít jednoduchou funkci a použít skládání jako lepidlo na vytvarování složitějších funkcí. Nicméně někdy může být zápis funkce v pointfree stylu méně čitelný, pokud je funkce příliš komplikovaná. To je důvod, proč se nedoporučuje dělat dlouhé řetězce poskládaných funkcí, ačkoliv se přiznávám, že se občas ve skládání funkcí vyžívám. Preferovaný styl je používat konstrukci let pro označování mezivýsledků nebo rozdělení problému na podproblémy a poté je dát dohromady, místo vytváření dlouhých řetězců funkcí, aby to dávalo smysl i případnému čtenáři.

V sekci o mapách a filtrech jsme řešili problém hledání součtu všech lichých čtverců, které byly menší než 10000. Takto vypadá řešení, když se vloží do funkce.

oddSquareSum :: Integer
oddSquareSum = sum (takeWhile (<10000) (filter odd (map (^2) [1..])))

Jako fanoušek skládání funkcí bych to nejspíš zapsal takhle:

oddSquareSum :: Integer
oddSquareSum = sum . takeWhile (<10000) . filter odd . map (^2) $ [1..]

Nicméně kdyby byla šance, že někdo jiný bude číst můj kód, napsal bych to asi takhle:

oddSquareSum :: Integer
oddSquareSum =
    let oddSquares = filter odd $ map (^2) [1..]
        belowLimit = takeWhile (<10000) oddSquares
    in  sum belowLimit

Nevyhrál bych s tím žádný programátorský turnaj, ale člověk, co by to četl, by to patrně považoval za čitelnější než řetězec poskládaných funkcí.