Začínáme
Připravit, pozor, teď!
Fajn, tak začneme! Pokud patříte do skupiny těch hrozných osob, které nečtou úvody do čehokoliv, a přeskočili ho, možná byste si stejně měli přečíst poslední část úvodu, protože se tam vysvětluje, co je potřeba na práci s tímto tutoriálem a jak budeme načítat soubory s funkcemi. První věc, kterou se budeme zabývat, je spuštění interaktivního módu GHC a zavolání nějakých funkcí, abyste se spřátelili s Haskellem. Spusťte si terminál a zadejte do něj ghci. Vypíše se zhruba takovéto uvítání:
GHCi, version 6.10.1: http://www.haskell.org/ghc/ :? for help Loading package ghc-prim ... linking ... done. Loading package integer ... linking ... done. Loading package base ... linking ... done. Prelude>
Gratuluji, jste v GHCi! Prompt je tady Prelude>, ale protože se může prodloužit po načtení nějakých dalších věcí, budeme dále používat ghci>. Pokud chcete mít stejný prompt, stačí napsat příkaz :set prompt "ghci> ".
Tady je příklad nějaké jednoduché aritmetiky.
ghci> 2 + 15 17 ghci> 49 * 100 4900 ghci> 1892 - 1472 420 ghci> 5 / 2 2.5 ghci>
Tohle je celkem samozřejmé. Můžeme také použít více operátorů na jednom řádku a ukázat si obvyklou prioritu operátorů. Můžeme použít závorky z důvodů explicitnosti nebo pro změnu priority.
ghci> (50 * 100) - 4999 1 ghci> 50 * 100 - 4999 1 ghci> 50 * (100 - 4999) -244950
Docela pěkné, co? Jo, vím, že není, ale vydržte to se mnou. Malá záludnost, na kterou je třeba si dát pozor, jsou záporná čísla. Pokud chceme pracovat se záporným číslem, je vždycky lepší jej obklopit závorkami. Při pokusu o výraz 5 * -3 bude na vás GHCi řvát, ale výraz 5 * (-3) bude fungovat dobře.
Booleova algebra je také celkem jasná. Jak pravděpodobně víte, && znamená booleovské a, || znamená booleovské nebo. Pomocí not se neguje True (pravda) nebo False (nepravda).
ghci> True && False False ghci> True && True True ghci> False || True True ghci> not False True ghci> not (True && True) False
Testování na rovnost se dělá nějak takhle.
ghci> 5 == 5 True ghci> 1 == 0 False ghci> 5 /= 5 False ghci> 5 /= 4 True ghci> "ahoj" == "ahoj" True
A co zkusit zadat výraz 5 + "lama" nebo 5 == True? No, pokud zkusíme první kus kódu, dostaneme velkou strašidelnou chybovou zprávu!
No instance for (Num [Char]) arising from a use of `+' at <interactive>:1:0-9 Possible fix: add an instance declaration for (Num [Char]) In the expression: 5 + "lama" In the definition of `it': it = 5 + "lama"
Jejda! GHCi se nám snaží sdělit, že "lama" není číslo a tak by se neměla přičítat k číslu 5. I kdyby to nebyla "lama", ale "čtyřka" nebo "4", Haskell by to pořád nepovažoval za číslo. Operátor + očekává, že na pravé a levé straně budou čísla. Pokud se pokusíme zadat True == 5, GHCi nám sdělí, že nám nesouhlasí typy. Zatímco + funguje jenom na číslech, == funguje na jakýchkoliv dvou věcech, které se dají porovnávat. Háček je v tom, že oba musí mít odpovídající typ. Nemůžete porovnávat jablka s hruškami. Na typy se podíváme blíže později. Poznámka: můžete provést 5 + 4.0, protože pětka je záludná a může se vydávat za celé nebo reálné číslo. Kdežto 4.0 se nemůže vydávat za celé číslo, takže se 5 musí přizpůsobit.
Možná to nevíte, ale teď jsme tu celou dobu používali funkce. Například * je funkce, která bere dvě čísla a násobí je. Jak jste viděli, zavoláme ji vecpáním mezi ně. Tomu se říká infixová funkce. Většina funkcí, které nepracují s čísly, jsou prefixové funkce. Podívejme se na ně.
Funkce jsou většinou prefixové, takže i když od teď explicitně neuvedeme, že je to funkce v prefixové formě, budeme ji za ni považovat. Ve většině imperativních jazyků jsou funkce zavolány napsáním názvu funkce a poté parametrů v závorkách, často oddělených čárkami. V Haskellu jsou funkce zavolány napsáním názvu funkce, mezery, a poté parametrů, oddělených mezerami. Pro začátek zkusíme zavolat jednu z nejnudnějších funkcí v Haskellu.
ghci> succ 8 9
Funkce succ požaduje jako parametr cokoliv, co má definováno následníka a následně ho vrátí. Jak můžete vidět, oddělili jsme název funkce od parametru mezerou. Zavoláním funkce s více parametry je také jednoduché. Funkce min a max vezmou dvě věci, které se dají porovnat (jako třeba čísla!) a vrátí menší nebo větší z nich.
ghci> min 9 10 9 ghci> min 3.4 3.2 3.2 ghci> max 100 101 101
Aplikace funkcí (zavolání funkce vložením mezery za ní a přidáním parametrů) má největší přednost ze všeho. Což pro nás znamená, že tyto dva výrazy jsou stejné.
ghci> succ 9 + max 5 4 + 1 16 ghci> (succ 9) + (max 5 4) + 1 16
Nicméně pokud chceme získat následníka součinu čísel 9 a 10, neměli bychom psát succ 9 * 10, protože to bychom získali následníka devítky, který by byl násoben desítkou. Tedy číslo 100. Museli bychom napsat succ (9 * 10), abychom obdrželi číslo 91.
Pokud funkce požaduje dva parametry, můžeme ji zavolat také infixově, když ji obklopíme zpětnými apostrofy. Například funkce div vezme dvě celá čísla a provede s nimi celočíselné dělení. Provedením div 92 10 dostaneme výsledek 9. Pokud to zapíšeme tímto způsobem, může to vést k nejasnostem, které číslo je dělenec a které dělitel. Můžeme tedy funkci zavolat infixově jako 92 `div` 10, což je hned jasnější.
Hodně lidí, kteří přešli k Haskellu z imperativních jazyků, se snaží držet zápisu, ve kterém závorky znázorňují aplikaci funkce. Kupříkladu v jazyce C se používají závorky na zavolání funkcí jako foo(), bar(1) nebo baz(3, "haha"). Jak jsme již uvedli, pro aplikaci funkce je používána v Haskellu mezera. Tyto funkce by v Haskellu byly zapsány jako foo, bar 1 a baz 3 "haha". Takže pokud uvidíte něco jako bar (bar 3), tak to neznamená, že bar je zavoláno s parametry bar a 3. Znamená to, že nejprve zavoláme funkci bar s parametrem 3, abychom obdrželi nějaké číslo, a pak na něj znovu zavolali bar. V C by to vypadalo zhruba jako bar(bar(3)).
Miminko má svou první funkci
V předchozí sekci jsme si vyzkoušeli volání funkcí. A teď si zkusíme vytvořit vlastní! Spusťte si svůj oblíbený editor a naťukejte tam následující funkci, která vezme číslo a vynásobí ho dvěma.
doubleMe x = x + x
Funkce jsou definovány podobným způsobem, jako jsou volány. Název funkce je následován parametry, oddělenými mezerami. Ale při definování funkce následuje =, za kterým určíme, co funkce dělá. Uložte si kód jako miminko.hs nebo tak nějak. Nyní přejděte do adresáře, ve kterém je uložen, a spusťte v něm ghci. Jakmile budete v GHCi, napište :l miminko. Jakmile se náš skript načte, můžeme si hrát s funkcí, jež jsme definovali.
ghci> :l miminko [1 of 1] Compiling Main ( miminko.hs, interpreted ) Ok, modules loaded: Main. ghci> doubleMe 9 18 ghci> doubleMe 8.3 16.6
Protože + funguje s celými i s desetinnými čísly (s čímkoliv, co se dá považovat za číslo, vážně), naše funkce budou také fungovat s jakýmkoliv číslem. Vytvořme si funkci, která vezme dvě čísla a vynásobí je dvojkou a poté je sečte.
doubleUs x y = x*2 + y*2
Jednoduché. Také bychom to mohli definovat jako doubleUs x y = x + x + y + y. Vyzkoušení přinese očekávaný výsledek (nezapomeňte přidat tuto funkci do souboru miminko.hs, uložit jej a poté napsat :l miminko v GHCi).
ghci> doubleUs 4 9 26 ghci> doubleUs 2.3 34.2 73.0 ghci> doubleUs 28 88 + doubleMe 123 478
Jak se dalo čekat, je možné volat funkci z jiných funkcí, které jste si vytvořili. Můžeme toho využít a předefinovat funkci doubleUs následovně:
doubleUs x y = doubleMe x + doubleMe y
Tohle je velmi jednoduchý příklad běžného schéma, jaké uvidíte všude v Haskellu. Vytvoření základní funkce, která je očividně správná, a pak je poskládána do více složitých funkcí. Takto se také vyhneme opakování. Co když nějaký matematik přijde na to, že dvojka je ve skutečnosti trojka a budete muset upravit svůj program? Stačí předefinovat doubleMe na x + x + x a protože doubleUs volá funkci doubleMe, mělo by to automaticky fungovat i v tom divném světě, kde je dvojka trojkou.
Funkce v Haskellu nemusí mít konkrétní pořadí, takže nezáleží, když definujete nejprve doubleMe a teprve poté doubleUs, nebo pokud to uděláte obráceně.
A teď vytvoříme funkci, která násobí číslo dvojkou, pokud to číslo je menší nebo rovno 100, protože čísla větší než 100 jsou pro nás dost velké!
doubleSmallNumber x = if x > 100
then x
else x*2
Tady jsme ukázali haskellový výraz if. Pravděpodobně znáte if z jiných jazyků. Rozdíl mezi tím v Haskellu a tím v imperativních jazycích je v tom, že část s else je v Haskellu povinná. V imperativních jazycích můžete přeskočit několik kroků, pokud není podmínka splněna, ale v Haskellu musí každý výraz a funkce něco vracet. Mohli bychom mít napsaný podmíněný výraz na jednom řádku, ale já pokládám první způsob za více přehledný. Další věc ohledně if v Haskellu: jedná se o výraz. Výraz je v podstatě kus kódu, který vrací hodnotu. Například 5 je výraz, protože vrací 5, 4 + 8 je výraz, x + y je také výraz, protože vrací součet x a y. Jelikož je else povinné, výraz if vždycky něco vrátí a proto je také výraz. Pokud chceme přidat jedničku ke každému číslu, které je vráceno naší předchozí funkcí, mohli bychom ji napsat zhruba takto.
doubleSmallNumber' x = (if x > 100 then x else x*2) + 1
Pokud bychom zanedbali závorky, přidali bychom jedničku pouze pokud by x nebylo větší než 100. Všimněte si čáry ' na konci názvu funkce. Apostrof nemá v Haskellu žádný speciální syntaktický význam. Je to znak, který se dá použít v názvu funkce. Obvykle používáme ' k označení striktní verzi funkce (která není líná), nebo lehce změněnou verzi funkce nebo proměnné. Protože je ' povolený znak v názvu funkce, můžeme vytvořit takovou funkci.
conanO'Brien = "To jsem já, Conan O'Brien!"
Jsou tu dvě pozoruhodné věci. První je, že v názvu funkce jsme Conanovo jméno nenapsali velkým písmenem. Je to proto, že funkce by jím neměly začínat. Proč tomu tak je, zjistíme později. Druhá věc je, že tahle funkce nepožaduje žádné parametry. Funkci bez parametrů se obvykle říká definice (nebo pojmenování). Protože nemůžeme měnit význam pojmenování (a funkce) po jejich definování, conanO'Brien a řetězec "To jsem já, Conan O'Brien!" se mohou při použití zaměňovat.
Úvod do seznamů
Stejně jako nákupní seznamy v reálném světě, seznamy v Haskellu jsou velmi užitečné. Je to nejvíce používaná datová struktura a může být použita na mnoho různých způsobů pro modelování a řešení spoustu problémů. Seznamy jsou TAK skvělé. V této sekci se podíváme na základy práce se seznamy, řetězce (které jsou také seznamy) a na generátor seznamu.
V Haskellu jsou seznamy homogenní datová struktura. Ukládá několik prvků stejného typu. Což znamená, že můžeme mít seznam čísel nebo seznam znaků, ale nemůžeme mít seznam, který obsahuje několik čísel a poté několik znaků. A nyní, seznam!
ghci> let lostNumbers = [4,8,15,16,23,42] ghci> lostNumbers [4,8,15,16,23,42]
Jak můžete vidět, seznamy se zadávají pomocí hranatých závorek a hodnoty se z nich oddělují čárkami. Pokud vyzkoušíte vytvořit seznam jako [1,2,'a',3,'b','c',4], Haskell si bude stěžovat, že znaky (které se mimochodem zapisují pomocí znaku mezi jednoduchými uvozovkami) nejsou čísla. Když už mluvíme o znacích, tak textové řetezce jsou jenom seznamy znaků. Zápis "ahoj" je pouze syntaktický cukr (zkrácený zápis) pro řetězec ['a','h','o','j']. Protože řetězce jsou seznamy, můžeme na ně používat funkci pro práci se seznamy, což je velmi šikovné.
Běžná úloha je spojení dvou seznamů dohromady. To se dělá pomocí operátoru ++.
ghci> [1,2,3,4] ++ [9,10,11,12] [1,2,3,4,9,10,11,12] ghci> "ahoj" ++ " " ++ "světe" "ahoj světe" ghci> ['k','v'] ++ ['á','k'] "kvák"
Poznámka překladatele: je možné, že GHCi vypíše místo diakritiky v řetězci hromadu divných čísel. Kupříkladu řetězec "Příliš žluťoučký kůň úpěl ďábelské ódy." se zobrazí jako "P\345\237li\353 \382lu\357ou\269k\253 k\367\328 \250p\283l \271\225belsk\233 \243dy.". Je to z důvodů převodu UTF-8 řetězců na ASCII. Řešením je použít knihovnu utf8-string, která se postará o správnou interpretaci, ale pro účely tohoto tutoriálu bude asi lepší to nechat být a ignorovat to, popřípadě psát příklady bez diakritiky.
Pozor na opakované používání operátoru ++ na dlouhé seznamy. Pokud spojujete dva seznamy (i když připojujete jednoprvkový seznam k delšímu seznamu, tedy například: [1,2,3] ++ [4]), Haskell musí interně projít přes celý seznam na levé straně od ++. To není problém, pokud pracujeme s krátkými seznamy. Ale přidávat něco na konec seznamu, který má pět miliónů položek, bude chvíli trvat. Každopádně vložení prvku na začátek seznamu pomocí operátoru : je okamžité.
ghci> '1':" KOČIČKA" "1 KOČIČKA" ghci> 5:[1,2,3,4,5] [5,1,2,3,4,5]
Všimněte si, že : vezme jako argument číslo a seznam čísel nebo znak a seznam znaků, kdežto ++ dva stejné seznamy. I kdybyste chtěli přidat jeden prvek na konec seznamu pomocí ++, musí být obklopený hranatými závorkami, aby byl seznam.
Výraz [1,2,3] je vlastně syntaktický cukr pro 1:2:3:[]. Dvě hranaté závorky [] jsou prázdný seznam. Když k nim připojíme 3 stane se z toho [3]. Jestliže připojíme k tomu 2 stane se z toho [2,3] a tak dále.
Poznámka: [], [[]] a [[],[],[]] jsou tři odlišné věci. To první je prázdný seznam, to druhé je seznam obsahující jeden prázdný seznam a to třetí je seznam, který obsahuje tři prázdné seznamy.
Pokud chcete získat ze seznamu prvek na nějaké pozici, použijte !!. Číslování indexu začíná od nuly.
ghci> "Steve Buscemi" !! 6 'B' ghci> [9.4,33.2,96.2,11.2,23.25] !! 1 33.2
Pokud se ale budete snažit získat šestý prvek ze seznamu, který má pouze čtyři prvky, dostanete chybovou hlášku, takže opatrně!
Seznamy mohou také obsahovat seznamy. Taktéž mohou obsahovat seznamy obsahující seznamy obsahující seznamy…
ghci> let b = [[1,2,3,4],[5,3,3,3],[1,2,2,3,4],[1,2,3]] ghci> b [[1,2,3,4],[5,3,3,3],[1,2,2,3,4],[1,2,3]] ghci> b ++ [[1,1,1,1]] [[1,2,3,4],[5,3,3,3],[1,2,2,3,4],[1,2,3],[1,1,1,1]] ghci> [6,6,6]:b [[6,6,6],[1,2,3,4],[5,3,3,3],[1,2,2,3,4],[1,2,3]] ghci> b !! 2 [1,2,2,3,4]
Seznamy uvnitř seznamu mohou být rozdílné délky, ale nesmí být jiného typu. Stejně jako nemůže být seznam obsahující několik znaků a několik čísel, nemůže být seznam, který obsahuje několik seznamů znaků a několik seznamů čísel.
Seznamy mohou být porovnávány, pokud je porovnatelný jejich obsah. Při používání <, <=, > a >= jsou seznamy porovnávány v lexikografickém pořadí. Nejprve jsou porovnány první prvky seznamů. Jestliže jsou stejné, pak jsou porovnány druhé prvky atd.
ghci> [3,2,1] > [2,1,0] True ghci> [3,2,1] > [2,10,100] True ghci> [3,4,2] > [3,4] True ghci> [3,4,2] > [2,4] True ghci> [3,4,2] == [3,4,2] True
Co dalšího můžeme dělat se seznamy? Zde jsou některé základní funkce na práci se seznamy.
Funkce head vezme seznam a vrátí jeho první prvek (hlavu seznamu).
ghci> head [5,4,3,2,1] 5
Funkce tail vezme seznam a vrátí jeho zbytek, což je vlastně všechno kromě prvního prvku.
ghci> tail [5,4,3,2,1] [4,3,2,1]
Funkce last vezme seznam a vrátí jeho poslední prvek.
ghci> last [5,4,3,2,1] 1
Funkce init vezme seznam a vrátí všechno kromě jeho posledního prvku.
ghci> init [5,4,3,2,1] [5,4,3,2]
Pokud budeme seznam považovat za příšeru, bude to asi takovéhle.
Ale co se stane, když budeme chtít první prvek z prázdného seznamu?
ghci> head [] *** Exception: Prelude.head: empty list
Pane jo! Úplně se nám to vymklo kontrole! Pokud není příšera, nemůže mít ani začátek. Při použití funkcí head, tail, last a init dávejte pozor, aby nebyly použity na prázdný seznam. Tato chyba nemůže být odchycena v čase překladu, takže je potřeba dávat pozor, aby se náhodou nepřikázalo Haskellu vybrat prvky z prázdného seznamu.
Funkce length vezme seznam a vrátí jeho délku.
ghci> length [5,4,3,2,1] 5
Funkce null zjistí, jestli je seznam prázdný. Pokud ano, vrací True, v opačném případě False. Používejte tuto funkci místo xs == [] (pokud máte seznam pojmenovaný xs).
ghci> null [1,2,3] False ghci> null [] True
Funkce reverse obrátí seznam.
ghci> reverse [5,4,3,2,1] [1,2,3,4,5]
Funkce take požaduje číslo a seznam. Vezme ze začátku seznamu tolik prvků, kolik je zadáno. Sledujte.
ghci> take 3 [5,4,3,2,1] [5,4,3] ghci> take 1 [3,9,3] [3] ghci> take 5 [1,2] [1,2] ghci> take 0 [6,6,6] []
Všimněte si, že pokud zkusíme vzít ze seznamu více prvků, než v něm je, prostě vrátí celý seznam. Jestliže zkusíme vzít 0 prvků, získáme tím prázdný seznam.
Funkce drop funguje podobně, akorát zahodí určitý počet prvků ze začátku seznamu.
ghci> drop 3 [8,4,2,1,5,6] [1,5,6] ghci> drop 0 [1,2,3,4] [1,2,3,4] ghci> drop 100 [1,2,3,4] []
Funkce maximum vezme seznam věcí, které se dají porovnat, a vrátí největší prvek.
Funkce minimum vrátí nejmenší prvek.
ghci> minimum [8,4,2,1,5,6] 1 ghci> maximum [1,9,2,3,4] 9
Funkce sum vezme seznam čísel a vrátí jejich součet.
Funkce product vezme seznam čísel a vrátí jejich součin.
ghci> sum [5,2,1,6,3,2,5,7] 31 ghci> product [6,2,1,2] 24 ghci> product [1,2,5,6,7,9,2,0] 0
Funkce elem vezme věc a seznam věcí a sdělí nám, jestli je ta věc prvkem seznamu. Je většinou volána jako infixová funkce, protože je jednodušší ji tak číst.
ghci> 4 `elem` [3,4,5,6] True ghci> 10 `elem` [3,4,5,6] False
Tohle bylo pár základních funkcí na práci se seznamy. Na více funkcí se podíváme v následujících sekcích.
Šerifovy rozsahy
Co když budeme chtít seznam všech čísel mezi jedničkou a dvacítkou? Určitě bychom je mohli všechny prostě napsat, ale to není zřejmě řešení pro džentlmeny, kteří požadují od svých programovacích jazyků dokonalost. Místo toho použijeme rozsahy. Rozsahy jsou způsob vytváření seznamů, které jsou aritmetické posloupnosti prvků, které se dají vyjmenovat. Čísla mohou být vyjmenována. Jedna, dva, tři, čtyři atd. Znaky mohou být také vyjmenovány. Abeceda je posloupnost znaků od A do Z (česká abeceda je od A do Ž). Jména nemůžou být vyjmenována. Co následuje po jménu „Jan“? Nevím.
Pro vytvoření seznamu všech přirozených čísel od jedničky do dvacítky stačí napsat [1..20]. To je stejné, jako bychom napsali [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20] a není rozdíl mezi tímto zápisem a předchozím, kromě toho, že vypisování dlouhých posloupností ručně je hloupé.
ghci> [1..20] [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20] ghci> ['a'..'z'] "abcdefghijklmnopqrstuvwxyz" ghci> ['K'..'Z'] "KLMNOPQRSTUVWXYZ"
Rozsahy jsou skvělé, protože se v nich také dá uvést přírůstek. Co když chceme všechna sudá čísla mezi jedničkou a dvacítkou? Nebo každé třetí číslo mezi jedničkou a dvacítkou?
ghci> [2,4..20] [2,4,6,8,10,12,14,16,18,20] ghci> [3,6..20] [3,6,9,12,15,18]
Je to jednoduše otázka oddělení prvních dvou prvků čárkou a potě stanovení horní meze. I když to je celkem chytré, rozsahy nedovedou dělat věci, které od nich někteří lidé očekávají. Nemůžete napsat [1,2,4,8,16..100] a očekávat, že tím získáte všechny mocniny dvojky. Za prvé protože můžete pouze uvést pouze jeden přírůstek. A za druhé protože některé nearitmetické posloupnosti jsou víceznačné, pokud zadáme pouze několik jejich prvních členů.
Pro vytvoření seznamu všech čísel od dvacítky do jedničky nestačí napsat [20..1], musíte uvést [20,19..1].
Pozor na vytváření rozsahů desetinných čísel! Protože nejsou (už z definice) naprosto přesné, jejich používání v rozsazích může vést k celkem divokým výsledkům.
ghci> [0.1, 0.3 .. 1] [0.1,0.3,0.5,0.7,0.8999999999999999,1.0999999999999999]
Moje rada je nepoužívat je v rozsazích.
Můžete také pomocí rozsahů vytvářet nekonečné seznamy jednoduše tím, že nestanovíte horní mez. Později se budeme zabývat detailněji nekonečnými seznamy. Teď pojďme prozkoumat, jak dostat prvních 24 násobků třináctky. Jasně, mohli bychom napsat [13,26..24*13]. Ale existuje lepší způsob: take 24 [13,26..]. Protože je Haskell líný, nebude se snažit vyhodnotit nekonečný seznam okamžitě, protože by s vyhodnocováním nikdy neskončil. Raději počká, co se všechno z toho nekonečného seznamu bude chtít. A uvidí, že chcete pouze prvních 24 prvků, které s radostí vrátí.
Užitečné funkce, které vytváří nekonečné seznamy:
Funkce cycle vezme seznam a opakuje (cyklí) ho nekonečně dlouho. Pokud si chcete výsledný seznam zobrazit, bude pořád pokračovat, takže si ho budete muset někde ukrojit.
ghci> take 10 (cycle [1,2,3]) [1,2,3,1,2,3,1,2,3,1] ghci> take 12 (cycle "LOL ") "LOL LOL LOL "
Funkce repeat vezme prvek a vytvoří z něj nekonečný seznam, obsahující pouze ten prvek.
ghci> take 10 (repeat 5) [5,5,5,5,5,5,5,5,5,5]
Ačkoliv je jednodušší použít funkci replicate, pokud chceme určitý počet opakování jednoho prvku v seznamu. Například replicate 3 10 vrátí [10,10,10].
Jsem generátor seznamu
Pokud jste někdy absolvovali matematický kurz, možná jste už slyšeli o intenzionálním zápisu množin. Ten se běžně používá pro generování určitých množin. Jednoduchý zápis množiny, jež obsahuje prvních deset sudých přirozených čísel, je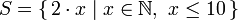 
. Část před svislítkem se nazývá výstupní funkce, x je proměnná, N je vstupní množina a x <= 10 je predikát. To znamená, že množina obsahuje dvojnásobek všech přirozených čísel, které vyhovují predikátu.
Pokud to budeme chtít vyjádřit v Haskellu, můžeme zkusit něco jako take 10 [2,4..]. Ale co když nebudeme chtít dvojnásobky prvních deseti přirozených čísel, ale něco mnohem složitějšího? Mohli bychom ten seznam definovat intenzionálně, tedy ho vygenerovat. Generátor seznamu je velmi podobný intenzionálnímu zápisu množin. Budeme se zatím držet výpisu prvních deseti sudých čísel. Intenzionálně to můžeme zapsat jako [x*2 | x <- [1..10]]. Hodnota x je brána z rozsahu [1..10] a pro každý prvek z [1..10] (jež je vázaný na x) dostaneme naši hodnotu, akorát vynásobenou dvojkou. Tady je generátor seznamu v akci.
ghci> [x*2 | x <- [1..10]] [2,4,6,8,10,12,14,16,18,20]
Jak můžete vidět, dostaneme požadovaný výsledek. Nyní si přidáme podmínku (nebo také predikát) do naší definice generátoru. Predikáty se zapisují až za část s navázáním proměnné a odděluje se čárkou. Řekněme, že bychom chtěli pouze prvky, jejichž dvojnásobek je větší nebo rovný dvanácti.
ghci> [x*2 | x <- [1..10], x*2 >= 12] [12,14,16,18,20]
Skvělé, funguje to. A co když budeme chtít všechna čísla od 50 do 100, jejichž zbytek po dělení číslem 7 je 3? Jednoduché.
ghci> [ x | x <- [50..100], x `mod` 7 == 3] [52,59,66,73,80,87,94]
Úspěch! Zapamatujte si, že se třídění seznamů pomocí predikátů také nazývá filtrování. Vezmeme seznam čísel a vyfiltrujeme je pomocí predikátů. A teď další příklad. Řekněme, že chceme vygenerovat přepsání každého lichého čísla většího než 10 řetězcem "BANG!" a každého lichého čísla, které je menší než 10, řetězcem "BOOM!". Pokud číslo není liché, zahodíme ho. Z důvodů pohodlnosti vložíme náš generátor do funkce, abychom ho mohli jednoduše použít vícekrát.
boomBangs xs = [ if x < 10 then "BOOM!" else "BANG!" | x <- xs, odd x]
Poslední část definice generátoru je predikát. Funkce odd vrací True, pokud je číslo liché, a False, pokud je sudé. Prvek je přidán do seznamu pouze pokud jsou všechny predikáty vyhodnoceny jako True.
ghci> boomBangs [7..13] ["BOOM!","BOOM!","BANG!","BANG!"]
Můžeme zapsat několik predikátů. Jestliže chceme všechna čísla od 10 do 20, která nejsou 13, 15 nebo 19, napíšeme:
ghci> [ x | x <- [10..20], x /= 13, x /= 15, x /= 19] [10,11,12,14,16,17,18,20]
Nejen že můžeme mít v definicích generátoru více predikátů (každý prvek musí splňovat veškeré predikáty, aby byl obsažen ve výsledném seznamu), můžeme také vybírat prvky z několika seznamů. Když vybíráme prvky z více seznamů, vygenerují se všechny kombinace ze zadaných seznamů a poté je můžeme zkombinovat ve výstupní funkci. Generátor seznamu, který bere prvky ze dvou seznamů délky 4, vrátí seznam délky 16, za předpokladu, že je nebude filtrovat. Pokud máme dva seznamy, [2,5,10] a [8,10,11] a budeme chtít součin všech možných kombinací čísel z těchto seznamů, uděláme následující.
ghci> [ x*y | x <- [2,5,10], y <- [8,10,11]] [16,20,22,40,50,55,80,100,110]
Jak jsme čekali, délka nového seznamu je 9. Co když budeme chtít všechny součiny, které jsou větší než 50?
ghci> [ x*y | x <- [2,5,10], y <- [8,10,11], x*y > 50] [55,80,100,110]
A co třeba generátor seznamu, který zkombinuje seznamy přídavných a podstatných jmen do bujaré epopeje?
ghci> let nouns = ["tulák","žabák","papež"] ghci> let adjectives = ["líný","nabručený","pletichářský"] ghci> [adjective ++ " " ++ noun | adjective <- adjectives, noun <- nouns] ["líný tulák","líný žabák","líný papež","nabručený tulák","nabručený žabák", "nabručený papež","pletichářský tulák","pletichářský žabák","pletichářský papež"]
Už vím! Napišme si vlastní verzi funkce length! Nazveme ji length'.
length' xs = sum [1 | _ <- xs]
Znak _ značí, že je nám jedno, co budeme dělat s prvkem ze seznamu, takže místo psaní názvu proměnné, kterou nikdy nepoužijeme, jednoduše napíšeme _. Tato funkce nahradí každý prvek v seznamu číslem 1 a poté je všechny sečte. Což znamená, že výsledný součet bude délka našeho seznamu.
Jenom přátelská připomínka: protože jsou řetězce seznamy, můžeme použít generátor seznamu na zpracování a vytváření řetězců. Zde je funkce, která vezme řetězce a odstraní z nich všechno kromě velkých písmen.
removeNonUppercase st = [ c | c <- st, c `elem` ['A'..'Z']]
Otestujeme ji:
ghci> removeNonUppercase "Hahaha! Ahahaha!" "HA" ghci> removeNonUppercase "neMAMRADZABY" "MAMRADZABY"
Veškerou práci zde zastává predikát. Vyjadřuje, že znak bude obsažen v novém seznamu pouze pokud je prvkem seznamu ['A'..'Z']. Zanořování generátorů je také možné, pokud operujete nad seznamy, jež obsahují další seznamy. Třeba seznam obsahující seznamy čísel. Pojďme odstranit všechna lichá čísla bez přeskupování seznamu.
ghci> let xxs = [[1,3,5,2,3,1,2,4,5],[1,2,3,4,5,6,7,8,9],[1,2,4,2,1,6,3,1,3,2,3,6]] ghci> [ [ x | x <- xs, even x ] | xs <- xxs] [[2,2,4],[2,4,6,8],[2,4,2,6,2,6]]
Generátor seznamu je možné zapsat přes několik řádků. Takže pokud zrovna nepracujete v GHCi, je lepší rozdělit dlouhé seznamy přes více řádků, zvláště když jsou zanořené.
N-tice
V některých ohledech jsou n-tice (uspořádané heterogenní seznamy o n prvcích) podobné seznamům — slouží pro ukládání několika hodnot do jedné. Jenomže mají pár zásadních odlišností. Seznam čísel je seznam čísel. To je jeho typ a nezáleží na tom, jestli obsahuje jedno číslo nebo nekonečně mnoho. N-tice se ovšem používají, pokud přesně víte, kolik hodnot chcete zkombinovat a jejich typ závisí na počtu a typu jednotlivých složek. Jsou uvozeny kulatými závorkami a jejich složky odděleny čárkami.
Další důležitou odlišností je, že nemusí být homogenní. Na rozdíl od seznamu může n-tice obsahovat kombinaci různých typů.
Zamysleme se nad tím, jak bychom v Haskellu vyjádřili dvourozměrnou souřadnici. Je možnost použít seznam. To by mohlo fungovat. Co když budeme chtít vložit pár vektorů do seznamu, abychom tak vyjádřili body nějakého útvaru na dvourozměrné ploše? Mohli bychom mít něco jako [[1,2],[8,11],[4,5]]. Problém s tímto způsobem spočívá v tom, že bychom z toho mohli udělat něco jako [[1,2],[8,11,5],[4,5]], s čímž Haskell nemá problém, jelikož to je stále seznam seznamů čísel, ale nedává to smysl. Ale n-tice o velikosti dva (nazývána jako dvojice) má svůj vlastní typ, což znamená, že seznam nemůže obsahovat několik dvojic a zároveň nějaké trojice (n-tice velikosti tři), takže ji použijeme místo toho. Namísto obklopování souřadnic hranatými závorkami použijeme kulaté: [(1,2),(8,11),(4,5)]. Co když se budeme snažit vytvořit útvar jako [(1,2),(8,11,5),(4,5)]? No, dostaneme tuhle chybu:
Couldn't match expected type `(t, t1)' against inferred type `(t2, t3, t4)' In the expression: (8, 11, 5) In the expression: [(1, 2), (8, 11, 5), (4, 5)] In the definition of `it': it = [(1, 2), (8, 11, 5), (4, 5)]
Říká nám to, že jsme se pokusili použít dvojici a trojici ve stejném seznamu, k čemuž by nemělo dojít. Stejně jako nemůžete vytvořit seznam jako [(1,2),("One",2)], protože první prvek v seznamu je dvojice čísel a druhý je dvojice sestávající se z řetězce a čísla. N-tice mohou být použity k vyjádření rozmanitých druhů dat. Kupříkladu pokud chceme v Haskellu vyjádřit někoho jméno a jeho věk, můžeme použít trojici: ("Christopher", "Walken", 55). Na tomto příkladu můžete vidět, že n-tice mohou obsahovat i seznamy.
Použijte n-tice, pokud předem víte, kolik složek budete na data potřebovat. N-tice jsou mnohem méně tvárné, protože se od počtu složek odvíjí jejich typ, takže nelze napsat obecnou funkci na přidání prvku do n-tice — musí se napsat funkce zvlášť pro dvojici, funkce pro trojici, pro čtveřici atd.
I když existuje jednoprvkový seznam, neexistuje věc jako n-tice s jednou složkou. Nedává to moc velký smysl, když se nad tím zamyslíte. Jednosložková n-tice by byla pouze hodnota, kterou by obsahovala, což by pro nás nemělo žádný přínos.
Stejně jako seznamy, n-tice se dají porovnávat, pokud jsou její složky porovnatelné. Nedají se ovšem porovnávat dvě n-tice rozdílné velikosti, zatím co je možné porovnávat dva rozdílně dlouhé seznamy. Dvě užitečné funkce, které pracují se dvojicemi:
Funkce fst vezme dvojici a vrátí její první složku.
ghci> fst (8,11)
8
ghci> fst ("Wow", False)
"Wow"
Funkce snd vezme dvojici a vrátí její druhou složku. Jaké překvapení!
ghci> snd (8,11)
11
ghci> snd ("Wow", False)
False
Skvělá funkce, která vytváří seznam dvojic: zip. Vezme dva seznamy a poté je sepne dohromady do seznamu spojením odpovídajích prvků do dvojic. Je to opravdu jednoduchá funkce, ale má hromadu použití. Je zvláště užitečná pro kombinaci nebo propojení dvou seznamů. Následuje názorná ukázka.
ghci> zip [1,2,3,4,5] [5,5,5,5,5] [(1,5),(2,5),(3,5),(4,5),(5,5)] ghci> zip [1 .. 5] ["jedna", "dva", "tři", "čtyři", "pět"] [(1,"jedna"),(2,"dva"),(3,"tři"),(4,"čtyři"),(5,"pět")]
Funkce spáruje prvky a vytvoří z nich nový seznam. První prvek s první, druhý s druhým atd. Všimněte si, že jelikož dvojice může obsahovat různorodé typy složek, zip taktéž může vzít dva typově různé seznamy a sepnout je dohromady. Co se stane, když délka seznamů nesouhlasí?
ghci> zip [5,3,2,6,2,7,2,5,4,6,6] ["já","jsem","želva"] [(5,"já"),(3,"jsem"),(2,"želva")]
Delší seznam se jednoduše ořízl, aby měl stejnou délku jako kratší. Protože je Haskell líný, můžeme párovat konečné seznamy s nekonečnými:
ghci> zip [1..] ["jablko", "pomeranč", "třešeň", "mango"] [(1,"jablko"),(2,"pomeranč"),(3,"třešeň"),(4,"mango")]
Zde je úloha, která kombinuje n-tice a generátor seznamu: jaký pravoúhlý trojúhelník s celočíselnými stranami má všechny strany rovné nebo menší než 10 a jeho obvod je 24? Nejprve zkusíme vypsat všechny trojúhelníky se stranami rovnými nebo menšími než 10:
ghci> let triangles = [ (a,b,c) | c <- [1..10], b <- [1..10], a <- [1..10] ]
Vygenerovali jsem si čísla ze tří seznamů a zkombinovali jsme je v naši výstupní funkci do trojic. Pokud v GHCi zadáte příkaz triangles, dostanete seznam všech možných trojúhelníků se stranami menšími nebo rovnými 10. Dále přidáme podmínku, že to musí být pravoúhlý trojúhelník. Taktéž upravíme tuto funkci přihlédnutím k faktu, že strana b není větší než přepona a že strana a není větší než strana b.
ghci> let rightTriangles = [ (a,b,c) | c <- [1..10], b <- [1..c], a <- [1..b], a^2 + b^2 == c^2]
Už jsme skoro hotovi. Teď jen změníme funkci prohlášením, že chceme jenom trojúhelníky s obvodem 24.
ghci> let rightTriangles' = [ (a,b,c) | c <- [1..10], b <- [1..c], a <- [1..b], a^2 + b^2 == c^2, a+b+c == 24] ghci> rightTriangles' [(6,8,10)]
A tady máme naši odpověď! Tohle je častý postup ve funkcionálním programování. Vezmete si počáteční množinu možných řešení a poté ji přetváříte a aplikujete filtry, dokud nezískáte správné řešení.