
Vytváříme si vlastní typy a typové třídy
Úvod do algebraických datových typů
Předchozí kapitoly se týkaly několika existujích haskellových typů a typových tříd. V této kapitole se naučíme vytvářet si naše vlastní a jak s nimi pracovat!
Do této chvíle jsme narazili na celou řadu datových typů. Bool, Int, Char, Maybe atd. Jak si ale vytvoříme své vlastní typy? Jeden způsob definice typu spočívá v použití klíčového slova data. Podívejme se, jak je ve standardní knihovně definován typ Bool.
data Bool = False | True
Klíčové slovo data uvádí definici nového datového typu. Následuje název definovaného typu, jímž je v tomto případě Bool. Napravo od rovnítka = jsou datové konstruktory. Ty určují přípustné hodnoty typu. Znak | se čte jako nebo. Zápis lze tedy číst jako: typ Bool může mít hodnotu True nebo False. Jak název typu, tak názvy konstruktorů musí začínat velkými písmeny.
Obdobně můžeme typ Int považovat za definovaný jako:
data Int = -2147483648 | -2147483647 | … | -1 | 0 | 1 | 2 | … | 2147483647

První a poslední datový konstruktor jsou nejnižší a nejvyšší možné hodnoty typu Int. Ve skutečnosti se takto nedefinují; trojtečky nahrazují hromadu čísel a máme to zde uvedeno pouze pro ilustraci.
Pojďme se nyní zamyslet nad tím, jak bychom vyjádřili tvary v Haskellu. Jednou možností je použití n-tic. Kružnici bychom zapsali jako (43.1, 55.0, 10.4), kde první a druhá složka jsou souřadnice středu kružnice a třetí je její poloměr. To vypadá nadějně, ale stejná čísla mohou také vyjadřovat třírozměrný vektor nebo cokoliv jiného. Lepším způsobem je vytvoření vlastního typu pro prezentaci tvaru. Řekněme, že tvarem bude kružnice, nebo obdélník. Tady to máme:
data Shape = Circle Float Float Float | Rectangle Float Float Float Float
Co je to zač? Uvažujme nad tím takhle. Datový konstruktor Circle má tři desetinná políčka. Takže když napíšeme datový konstruktor, můžeme za něj volitelně přidat nějaké typy a ty definují hodnoty, které bude obsahovat. Zde jsou první dvě políčka souřadnice středu kružnice, třetí je její poloměr. Datový konstruktor Rectangle má čtyři desetinná políčka. První dvě jsou souřadnice levého horního rohu, zbylé dvě souřadnice pravého dolního rohu obdélníku.
Když řeknu políčko, tak ve skutečnosti tím myslím parametr. Datové konstruktory jsou vlastně funkce, které vracejí hodnoty daného typu. Podívejme se na typ těchto dvou datových konstruktorů.
ghci> :t Circle Circle :: Float -> Float -> Float -> Shape ghci> :t Rectangle Rectangle :: Float -> Float -> Float -> Float -> Shape
Bezva, takže konstruktory jsou rovněž funkce. Kdo by si to pomyslel? Vytvořme funkci, která vezme hodnotu typu Shape a vrací jeho plochu.
surface :: Shape -> Float surface (Circle _ _ r) = pi * r ^ 2 surface (Rectangle x1 y1 x2 y2) = (abs $ x2 - x1) * (abs $ y2 - y1)
První pozoruhodnou věcí zde je deklarace typu. Ta říká, že funkce vezme tvar a vrací desetinné číslo. Nemůžeme napsat Circle -> Float, protože Circle není typ, zatímco Shape je. Stejně jako bychom nemohli napsat funkci typu True -> Int. Dále si zde povšimněme, že lze datové konstruktory využít jako vzor. Už předtím jsme používali ve vzorech kostruktory (ve skutečnosti celou dobu), když jsme tam zadávali hodnoty jako [], False nebo 5, jenom tyto hodnoty neměly žádné parametry. Jednoduše napíšeme konstruktor a poté pojmenujeme jeho parametry. Protože nás zajímá poloměr, nestaráme se o první dva, ty pouze udávají polohu kružnice:
ghci> surface $ Circle 10 20 10 314.15927 ghci> surface $ Rectangle 0 0 100 100 10000.0
Paráda, funguje to! Když ale zkusíme do příkazového řádku napsat Circle 10 20 5, vyhodí chybu. To protože Haskell (zatím) neví, jak znázornit náš datový typ. Pamatujte si, že když zkoušíme vypsat hodnotu do příkazového řádku, Haskell musí nejprve spustit funkci show, aby získal textovou reprezentaci naší hodnoty, a teprve poté ji vypíše v terminálu. Aby se náš datový typ Shape stal součástí typové třídy Show, upravíme jej takto:
data Shape = Circle Float Float Float | Rectangle Float Float Float Float deriving (Show)
Nebudeme se teď tím zabývat dopodrobna. Řekněme, že když napíšeme deriving (Show) na konec deklarace data, Haskell automaticky zahrne typ do typové třídy Show. Tím pádem teď můžeme udělat tohle:
ghci> Circle 10 20 5 Circle 10.0 20.0 5.0 ghci> Rectangle 50 230 60 90 Rectangle 50.0 230.0 60.0 90.0
Datové konstruktory jsou funkce, takže je můžeme částečně aplikovat a tak. Chceme-li seznam soustředných kružnic s různými poloměry, můžeme napsat toto:
ghci> map (Circle 10 20) [4,5,6,6] [Circle 10.0 20.0 4.0,Circle 10.0 20.0 5.0,Circle 10.0 20.0 6.0,Circle 10.0 20.0 6.0]
Náš datový typ je dobrý, i když by mohl být ještě lepší. Vytvořme pomocný datový typ pro definici bodu ve dvourozměrném prostoru. Ten pak můžeme použít pro přehlednější vytváření tvarů.
data Point = Point Float Float deriving (Show) data Shape = Circle Point Float | Rectangle Point Point deriving (Show)
Všimněte si, že jsme při definici bodu použili stejné jméno jak pro datový typ, tak pro datový konstruktor. Nemá to žádný zvláštní význam, přestože je obvyklé používat stejný název u typů s jedním datovým konstruktorem. Takže nyní má Circle dva parametry, jeden typu Point a druhý typu Float. Díky tomu jednodušeji porozumíme, co je co. Totéž platí pro obdélník. Musíme ovšem náležitě upravit funkci surface.
surface :: Shape -> Float surface (Circle _ r) = pi * r ^ 2 surface (Rectangle (Point x1 y1) (Point x2 y2)) = (abs $ x2 - x1) * (abs $ y2 - y1)
Jediná věc k úpravě byly vzory. Ignorovali jsme bod ve vzoru pro kruh. U vzoru pro obdélník jsme pomocí zanořených vzorů vytáhli jednotlivé parametry bodů. Kdybychom z nějakého důvodu chtěli pracovat s celým bodem, mohli bychom použít zástupný vzor.
ghci> surface (Rectangle (Point 0 0) (Point 100 100)) 10000.0 ghci> surface (Circle (Point 0 0) 24) 1809.5574
Což takhle vytvořit funkci, která bude náš tvar posunovat? Vezme tvar a délku posunů ve směru os x a y a vrátí nový tvar se stejnými rozměry, ale s jiným umístěním.
nudge :: Shape -> Float -> Float -> Shape nudge (Circle (Point x y) r) a b = Circle (Point (x+a) (y+b)) r nudge (Rectangle (Point x1 y1) (Point x2 y2)) a b = Rectangle (Point (x1+a) (y1+b)) (Point (x2+a) (y2+b))
Pěkně přímočaré. Přičítáme délku posunů k bodům, jež označují pozice bodů.
ghci> nudge (Circle (Point 34 34) 10) 5 10 Circle (Point 39.0 44.0) 10.0
Kdybychom se přímo nechtěli zabývat pozicemi bodů, mohli bychom vytvořit pomocné funkce, které vytvoří tvary ve výchozí pozici, a poté bychom je posunuli.
baseCircle :: Float -> Shape baseCircle r = Circle (Point 0 0) r baseRect :: Float -> Float -> Shape baseRect width height = Rectangle (Point 0 0) (Point width height)
ghci> nudge (baseRect 40 100) 60 23 Rectangle (Point 60.0 23.0) (Point 100.0 123.0)
Své datové typy můžete exportovat do vlastního modulu. Stačí vypsat typy spolu s funkcemi, které exportujeme, a pak přidat závorky a v nich uvést datové konstruktory k exportu oddělené čárkami. Chceme-li exportovat všechny datové konstruktory daného typu, stačí napsat ...
V našem případě bychom s exportováním začali takhle:
module Shapes ( Point(..) , Shape(..) , surface , nudge , baseCircle , baseRect ) where
Napsáním Shape(..) exportujeme všechny datové konstruktory typu Shape, což znamená, že kdokoli importuje náš modul, může vytvářet tvary spoužitím datových konstruktorů Rectangle a Circle. Je to totožné s napsáním Shape (Rectangle, Circle).
Můžeme také chtít, aby se žádné datové konstruktory typu Shape neexportovaly, a napsali bychom pouze Shape. V tom případě by bylo možné po importu vytvářet tvary pouze pomocí pomocných funkcí baseCircle a baseRect. Modul Data.Map využívá tento přístup. Není možné vytvářet asociační seznam napsáním Map.Map [(1,2),(3,4)], protože neexportuje svůj datový konstruktor. Nicméně lze vytvořit asociační seznam využitím pomocné funkce Map.fromList. Pamatujte si, že datové konstruktory jsou obyčejné funkce, které vezmou parametry a vrátí hodnotu určitého typu (například Shape) jako výsledek. Takže když se rozhodneme je neexportovat, pouze zabráníme osobě využívající náš modul je používat, ale pokud nějaká jiná exportovaná funkce vrací náš typ, může být využita k vytváření našeho datového typu.
Při nepovolení exportu datových kostruktorů se stanou datové typy více abstraktními ve smyslu, že skryjeme jejich implementace. Kromě toho, kdokoliv použije náš modul, nebude moct využít datové konstruktory ve vzorech.
Záznamy

OK, we've been tasked with creating a data type that describes a person. The info that we want to store about that person is: first name, last name, age, height, phone number, and favorite ice-cream flavor. I don't know about you, but that's all I ever want to know about a person. Let's give it a go!
data Person = Person String String Int Float String String deriving (Show)
O-kay. The first field is the first name, the second is the last name, the third is the age and so on. Let's make a person.
ghci> let guy = Person "Buddy" "Finklestein" 43 184.2 "526-2928" "Chocolate" ghci> guy Person "Buddy" "Finklestein" 43 184.2 "526-2928" "Chocolate"
That's kind of cool, although slightly unreadable. What if we want to create a function to get seperate info from a person? A function that gets some person's first name, a function that gets some person's last name, etc. Well, we'd have to define them kind of like this.
firstName :: Person -> String firstName (Person firstname _ _ _ _ _) = firstname lastName :: Person -> String lastName (Person _ lastname _ _ _ _) = lastname age :: Person -> Int age (Person _ _ age _ _ _) = age height :: Person -> Float height (Person _ _ _ height _ _) = height phoneNumber :: Person -> String phoneNumber (Person _ _ _ _ number _) = number flavor :: Person -> String flavor (Person _ _ _ _ _ flavor) = flavor
Whew! I certainly did not enjoy writing that! Despite being very cumbersome and BORING to write, this method works.
ghci> let guy = Person "Buddy" "Finklestein" 43 184.2 "526-2928" "Chocolate" ghci> firstName guy "Buddy" ghci> height guy 184.2 ghci> flavor guy "Chocolate"
There must be a better way, you say! Well no, there isn't, sorry.
Just kidding, there is. Hahaha! The makers of Haskell were very smart and anticipated this scenario. They included an alternative way to write data types. Here's how we could achieve the above functionality with record syntax.
data Person = Person { firstName :: String
, lastName :: String
, age :: Int
, height :: Float
, phoneNumber :: String
, flavor :: String
} deriving (Show)
So instead of just naming the field types one after another and separating them with spaces, we use curly brackets. First we write the name of the field, for instance, firstName and then we write a double colon :: (also called Paamayim Nekudotayim, haha) and then we specify the type. The resulting data type is exactly the same. The main benefit of this is that it creates functions that lookup fields in the data type. By using record syntax to create this data type, Haskell automatically made these functions: firstName, lastName, age, height, phoneNumber and flavor.
ghci> :t flavor flavor :: Person -> String ghci> :t firstName firstName :: Person -> String
There's another benefit to using record syntax. When we derive Show for the type, it displays it differently if we use record syntax to define and instantiate the type. Say we have a type that represents a car. We want to keep track of the company that made it, the model name and its year of production. Watch.
data Car = Car String String Int deriving (Show)
ghci> Car "Ford" "Mustang" 1967 Car "Ford" "Mustang" 1967
If we define it using record syntax, we can make a new car like this.
data Car = Car {company :: String, model :: String, year :: Int} deriving (Show)
ghci> Car {company="Ford", model="Mustang", year=1967}
Car {company = "Ford", model = "Mustang", year = 1967}
When making a new car, we don't have to necessarily put the fields in the proper order, as long as we list all of them. But if we don't use record syntax, we have to specify them in order.
Use record syntax when a constructor has several fields and it's not obvious which field is which. If we make a 3D vector data type by doing data Vector = Vector Int Int Int, it's pretty obvious that the fields are the components of a vector. However, in our Person and Car types, it wasn't so obvious and we greatly benefited from using record syntax.
Type parameters
A value constructor can take some values parameters and then produce a new value. For instance, the Car constructor takes three values and produces a car value. In a similar manner, type constructors can take types as parameters to produce new types. This might sound a bit too meta at first, but it's not that complicated. If you're familiar with templates in C++, you'll see some parallels. To get a clear picture of what type parameters work like in action, let's take a look at how a type we've already met is implemented.
data Maybe a = Nothing | Just a

The a here is the type parameter. And because there's a type parameter involved, we call Maybe a type constructor. Depending on what we want this data type to hold when it's not Nothing, this type constructor can end up producing a type of Maybe Int, Maybe Car, Maybe String, etc. No value can have a type of just Maybe, because that's not a type per se, it's a type constructor. In order for this to be a real type that a value can be part of, it has to have all its type parameters filled up.
So if we pass Char as the type parameter to Maybe, we get a type of Maybe Char. The value Just 'a' has a type of Maybe Char, for example.
You might not know it, but we used a type that has a type parameter before we used Maybe. That type is the list type. Although there's some syntactic sugar in play, the list type takes a parameter to produce a concrete type. Values can have an [Int] type, a [Char] type, a [[String]] type, but you can't have a value that just has a type of [].
Let's play around with the Maybe type.
ghci> Just "Haha" Just "Haha" ghci> Just 84 Just 84 ghci> :t Just "Haha" Just "Haha" :: Maybe [Char] ghci> :t Just 84 Just 84 :: (Num t) => Maybe t ghci> :t Nothing Nothing :: Maybe a ghci> Just 10 :: Maybe Double Just 10.0
Type parameters are useful because we can make different types with them depending on what kind of types we want contained in our data type. When we do :t Just "Haha", the type inference engine figures it out to be of the type Maybe [Char], because if the a in the Just a is a string, then the a in Maybe a must also be a string.
Notice that the type of Nothing is Maybe a. Its type is polymorphic. If some function requires a Maybe Int as a parameter, we can give it a Nothing, because a Nothing doesn't contain a value anyway and so it doesn't matter. The Maybe a type can act like a Maybe Int if it has to, just like 5 can act like an Int or a Double. Similarly, the type of the empty list is [a]. An empty list can act like a list of anything. That's why we can do [1,2,3] ++ [] and ["ha","ha","ha"] ++ [].
Using type parameters is very beneficial, but only when using them makes sense. Usually we use them when our data type would work regardless of the type of the value it then holds inside it, like with our Maybe a type. If our type acts as some kind of box, it's good to use them. We could change our Car data type from this:
data Car = Car { company :: String
, model :: String
, year :: Int
} deriving (Show)
To this:
data Car a b c = Car { company :: a
, model :: b
, year :: c
} deriving (Show)
But would we really benefit? The answer is: probably no, because we'd just end up defining functions that only work on the Car String String Int type. For instance, given our first definition of Car, we could make a function that displays the car's properties in a nice little text.
tellCar :: Car -> String
tellCar (Car {company = c, model = m, year = y}) = "This " ++ c ++ " " ++ m ++ " was made in " ++ show y
ghci> let stang = Car {company="Ford", model="Mustang", year=1967}
ghci> tellCar stang
"This Ford Mustang was made in 1967"
A cute little function! The type declaration is cute and it works nicely. Now what if Car was Car a b c?
tellCar :: (Show a) => Car String String a -> String
tellCar (Car {company = c, model = m, year = y}) = "This " ++ c ++ " " ++ m ++ " was made in " ++ show y
We'd have to force this function to take a Car type of (Show a) => Car String String a. You can see that the type signature is more complicated and the only benefit we'd actually get would be that we can use any type that's an instance of the Show typeclass as the type for c.
ghci> tellCar (Car "Ford" "Mustang" 1967) "This Ford Mustang was made in 1967" ghci> tellCar (Car "Ford" "Mustang" "nineteen sixty seven") "This Ford Mustang was made in \"nineteen sixty seven\"" ghci> :t Car "Ford" "Mustang" 1967 Car "Ford" "Mustang" 1967 :: (Num t) => Car [Char] [Char] t ghci> :t Car "Ford" "Mustang" "nineteen sixty seven" Car "Ford" "Mustang" "nineteen sixty seven" :: Car [Char] [Char] [Char]

In real life though, we'd end up using Car String String Int most of the time and so it would seem that parameterizing the Car type isn't really worth it. We usually use type parameters when the type that's contained inside the data type's various value constructors isn't really that important for the type to work. A list of stuff is a list of stuff and it doesn't matter what the type of that stuff is, it can still work. If we want to sum a list of numbers, we can specify later in the summing function that we specifically want a list of numbers. Same goes for Maybe. Maybe represents an option of either having nothing or having one of something. It doesn't matter what the type of that something is.
Another example of a parameterized type that we've already met is Map k v from Data.Map. The k is the type of the keys in a map and the v is the type of the values. This is a good example of where type parameters are very useful. Having maps parameterized enables us to have mappings from any type to any other type, as long as the type of the key is part of the Ord typeclass. If we were defining a mapping type, we could add a typeclass constraint in the data declaration:
data (Ord k) => Map k v = ...
However, it's a very strong convention in Haskell to never add typeclass constraints in data declarations. Why? Well, because we don't benefit a lot, but we end up writing more class constraints, even when we don't need them. If we put or don't put the Ord k constraint in the data declaration for Map k v, we're going to have to put the constraint into functions that assume the keys in a map can be ordered. But if we don't put the constraint in the data declaration, we don't have to put (Ord k) => in the type declarations of functions that don't care whether the keys can be ordered or not. An example of such a function is toList, that just takes a mapping and converts it to an associative list. Its type signature is toList :: Map k a -> [(k, a)]. If Map k v had a type constraint in its data declaration, the type for toList would have to be toList :: (Ord k) => Map k a -> [(k, a)], even though the function doesn't do any comparing of keys by order.
So don't put type constraints into data declarations even if it seems to make sense, because you'll have to put them into the function type declarations either way.
Let's implement a 3D vector type and add some operations for it. We'll be using a parameterized type because even though it will usually contain numeric types, it will still support several of them.
data Vector a = Vector a a a deriving (Show) vplus :: (Num t) => Vector t -> Vector t -> Vector t (Vector i j k) `vplus` (Vector l m n) = Vector (i+l) (j+m) (k+n) vectMult :: (Num t) => Vector t -> t -> Vector t (Vector i j k) `vectMult` m = Vector (i*m) (j*m) (k*m) scalarMult :: (Num t) => Vector t -> Vector t -> t (Vector i j k) `scalarMult` (Vector l m n) = i*l + j*m + k*n
vplus is for adding two vectors together. Two vectors are added just by adding their corresponding components. scalarMult is for the scalar product of two vectors and vectMult is for multiplying a vector with a scalar. These functions can operate on types of Vector Int, Vector Integer, Vector Float, whatever, as long as the a from Vector a is from the Num typeclass. Also, if you examine the type declaration for these functions, you'll see that they can operate only on vectors of the same type and the numbers involved must also be of the type that is contained in the vectors. Notice that we didn't put a Num class constraint in the data declaration, because we'd have to repeat it in the functions anyway.
Once again, it's very important to distinguish between the type constructor and the value constructor. When declaring a data type, the part before the = is the type constructor and the constructors after it (possibly separated by |'s) are value constructors. Giving a function a type of Vector t t t -> Vector t t t -> t would be wrong, because we have to put types in type declaration and the vector type constructor takes only one parameter, whereas the value constructor takes three. Let's play around with our vectors.
ghci> Vector 3 5 8 `vplus` Vector 9 2 8 Vector 12 7 16 ghci> Vector 3 5 8 `vplus` Vector 9 2 8 `vplus` Vector 0 2 3 Vector 12 9 19 ghci> Vector 3 9 7 `vectMult` 10 Vector 30 90 70 ghci> Vector 4 9 5 `scalarMult` Vector 9.0 2.0 4.0 74.0 ghci> Vector 2 9 3 `vectMult` (Vector 4 9 5 `scalarMult` Vector 9 2 4) Vector 148 666 222
Derived instances

In the Typeclasses 101 section, we explained the basics of typeclasses. We explained that a typeclass is a sort of an interface that defines some behavior. A type can be made an instance of a typeclass if it supports that behavior. Example: the Int type is an instance of the Eq typeclass because the Eq typeclass defines behavior for stuff that can be equated. And because integers can be equated, Int is a part of the Eq typeclass. The real usefulness comes with the functions that act as the interface for Eq, namely == and /=. If a type is a part of the Eq typeclass, we can use the == functions with values of that type. That's why expressions like 4 == 4 and "foo" /= "bar" typecheck.
We also mentioned that they're often confused with classes in languages like Java, Python, C++ and the like, which then baffles a lot of people. In those languages, classes are a blueprint from which we then create objects that contain state and can do some actions. Typeclasses are more like interfaces. We don't make data from typeclasses. Instead, we first make our data type and then we think about what it can act like. If it can act like something that can be equated, we make it an instance of the Eq typeclass. If it can act like something that can be ordered, we make it an instance of the Ord typeclass.
In the next section, we'll take a look at how we can manually make our types instances of typeclasses by implementing the functions defined by the typeclasses. But right now, let's see how Haskell can automatically make our type an instance of any of the following typeclasses: Eq, Ord, Enum, Bounded, Show, Read. Haskell can derive the behavior of our types in these contexts if we use the deriving keyword when making our data type.
Consider this data type:
data Person = Person { firstName :: String
, lastName :: String
, age :: Int
}
It describes a person. Let's assume that no two people have the same combination of first name, last name and age. Now, if we have records for two people, does it make sense to see if they represent the same person? Sure it does. We can try to equate them and see if they're equal or not. That's why it would make sense for this type to be part of the Eq typeclass. We'll derive the instance.
data Person = Person { firstName :: String
, lastName :: String
, age :: Int
} deriving (Eq)
When we derive the Eq instance for a type and then try to compare two values of that type with == or /=, Haskell will see if the value constructors match (there's only one value constructor here though) and then it will check if all the data contained inside matches by testing each pair of fields with ==. There's only one catch though, the types of all the fields also have to be part of the Eq typeclass. But since both String and Int are, we're OK. Let's test our Eq instance.
ghci> let mikeD = Person {firstName = "Michael", lastName = "Diamond", age = 43}
ghci> let adRock = Person {firstName = "Adam", lastName = "Horovitz", age = 41}
ghci> let mca = Person {firstName = "Adam", lastName = "Yauch", age = 44}
ghci> mca == adRock
False
ghci> mikeD == adRock
False
ghci> mikeD == mikeD
True
ghci> mikeD == Person {firstName = "Michael", lastName = "Diamond", age = 43}
True
Of course, since Person is now in Eq, we can use it as the a for all functions that have a class constraint of Eq a in their type signature, such as elem.
ghci> let beastieBoys = [mca, adRock, mikeD] ghci> mikeD `elem` beastieBoys True
The Show and Read typeclasses are for things that can be converted to or from strings, respectively. Like with Eq, if a type's constructors have fields, their type has to be a part of Show or Read if we want to make our type an instance of them. Let's make our Person data type a part of Show and Read as well.
data Person = Person { firstName :: String
, lastName :: String
, age :: Int
} deriving (Eq, Show, Read)
Now we can print a person out to the terminal.
ghci> let mikeD = Person {firstName = "Michael", lastName = "Diamond", age = 43}
ghci> mikeD
Person {firstName = "Michael", lastName = "Diamond", age = 43}
ghci> "mikeD is: " ++ show mikeD
"mikeD is: Person {firstName = \"Michael\", lastName = \"Diamond\", age = 43}"
Had we tried to print a person on the terminal before making the Person data type part of Show, Haskell would have complained at us, claiming it doesn't know how to represent a person as a string. But now that we've derived a Show instance for it, it does know.
Read is pretty much the inverse typeclass of Show. Show is for converting values of our a type to a string, Read is for converting strings to values of our type. Remember though, when we use the read function, we have to use an explicit type annotation to tell Haskell which type we want to get as a result. If we don't make the type we want as a result explicit, Haskell doesn't know which type we want.
ghci> read "Person {firstName =\"Michael\", lastName =\"Diamond\", age = 43}" :: Person
Person {firstName = "Michael", lastName = "Diamond", age = 43}
If we use the result of our read later on in a way that Haskell can infer that it should read it as a person, we don't have to use type annotation.
ghci> read "Person {firstName =\"Michael\", lastName =\"Diamond\", age = 43}" == mikeD
True
We can also read parameterized types, but we have to fill in the type parameters. So we can't do read "Just 't'" :: Maybe a, but we can do read "Just 't'" :: Maybe Char.
We can derive instances for the Ord type class, which is for types that have values that can be ordered. If we compare two values of the same type that were made using different constructors, the value which was made with a constructor that's defined first is considered smaller. For instance, consider the Bool type, which can have a value of either False or True. For the purpose of seeing how it behaves when compared, we can think of it as being implemented like this:
data Bool = False | True deriving (Ord)
Because the False value constructor is specified first and the True value constructor is specified after it, we can consider True as greater than False.
ghci> True `compare` False GT ghci> True > False True ghci> True < False False
In the Maybe a data type, the Nothing value constructor is specified before the Just value constructor, so a value of Nothing is always smaller than a value of Just something, even if that something is minus one billion trillion. But if we compare two Just values, then it goes to compare what's inside them.
ghci> Nothing < Just 100 True ghci> Nothing > Just (-49999) False ghci> Just 3 `compare` Just 2 GT ghci> Just 100 > Just 50 True
But we can't do something like Just (*3) > Just (*2), because (*3) and (*2) are functions, which aren't instances of Ord.
We can easily use algebraic data types to make enumerations and the Enum and Bounded typeclasses help us with that. Consider the following data type:
data Day = Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday
Because all the value constructors are nullary (take no parameters, i.e. fields), we can make it part of the Enum typeclass. The Enum typeclass is for things that have predecessors and successors. We can also make it part of the Bounded typeclass, which is for things that have a lowest possible value and highest possible value. And while we're at it, let's also make it an instance of all the other derivable typeclasses and see what we can do with it.
data Day = Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday
deriving (Eq, Ord, Show, Read, Bounded, Enum)
Because it's part of the Show and Read typeclasses, we can convert values of this type to and from strings.
ghci> Wednesday Wednesday ghci> show Wednesday "Wednesday" ghci> read "Saturday" :: Day Saturday
Because it's part of the Eq and Ord typeclasses, we can compare or equate days.
ghci> Saturday == Sunday False ghci> Saturday == Saturday True ghci> Saturday > Friday True ghci> Monday `compare` Wednesday LT
It's also part of Bounded, so we can get the lowest and highest day.
ghci> minBound :: Day Monday ghci> maxBound :: Day Sunday
It's also an instance of Enum. We can get predecessors and successors of days and we can make list ranges from them!
ghci> succ Monday Tuesday ghci> pred Saturday Friday ghci> [Thursday .. Sunday] [Thursday,Friday,Saturday,Sunday] ghci> [minBound .. maxBound] :: [Day] [Monday,Tuesday,Wednesday,Thursday,Friday,Saturday,Sunday]
That's pretty awesome.
Type synonyms
Previously, we mentioned that when writing types, the [Char] and String types are equivalent and interchangeable. That's implemented with type synonyms. Type synonyms don't really do anything per se, they're just about giving some types different names so that they make more sense to someone reading our code and documentation. Here's how the standard library defines String as a synonym for [Char].
type String = [Char]

We've introduced the type keyword. The keyword might be misleading to some, because we're not actually making anything new (we did that with the data keyword), but we're just making a synonym for an already existing type.
If we make a function that converts a string to uppercase and call it toUpperString or something, we can give it a type declaration of toUpperString :: [Char] -> [Char] or toUpperString :: String -> String. Both of these are essentially the same, only the latter is nicer to read.
When we were dealing with the Data.Map module, we first represented a phonebook with an association list before converting it into a map. As we've already found out, an association list is a list of key-value pairs. Let's look at a phonebook that we had.
phoneBook :: [(String,String)]
phoneBook =
[("betty","555-2938")
,("bonnie","452-2928")
,("patsy","493-2928")
,("lucille","205-2928")
,("wendy","939-8282")
,("penny","853-2492")
]
We see that the type of phoneBook is [(String,String)]. That tells us that it's an association list that maps from strings to strings, but not much else. Let's make a type synonym to convey some more information in the type declaration.
type PhoneBook = [(String,String)]
Now the type declaration for our phonebook can be phoneBook :: PhoneBook. Let's make a type synonym for String as well.
type PhoneNumber = String type Name = String type PhoneBook = [(Name,PhoneNumber)]
Giving the String type synonyms is something that Haskell programmers do when they want to convey more information about what strings in their functions should be used as and what they represent.
So now, when we implement a function that takes a name and a number and sees if that name and number combination is in our phonebook, we can give it a very pretty and descriptive type declaration.
inPhoneBook :: Name -> PhoneNumber -> PhoneBook -> Bool inPhoneBook name pnumber pbook = (name,pnumber) `elem` pbook
If we decided not to use type synonyms, our function would have a type of String -> String -> [(String,String)] -> Bool. In this case, the type declaration that took advantage of type synonyms is easier to understand. However, you shouldn't go overboard with them. We introduce type synonyms either to describe what some existing type represents in our functions (and thus our type declarations become better documentation) or when something has a long-ish type that's repeated a lot (like [(String,String)]) but represents something more specific in the context of our functions.
Type synonyms can also be parameterized. If we want a type that represents an association list type but still want it to be general so it can use any type as the keys and values, we can do this:
type AssocList k v = [(k,v)]
Now, a function that gets the value by a key in an association list can have a type of (Eq k) => k -> AssocList k v -> Maybe v. AssocList is a type constructor that takes two types and produces a concrete type, like AssocList Int String, for instance.
Just like we can partially apply functions to get new functions, we can partially apply type parameters and get new type constructors from them. Just like we call a function with too few parameters to get back a new function, we can specify a type constructor with too few type parameters and get back a partially applied type constructor. If we wanted a type that represents a map (from Data.Map) from integers to something, we could either do this:
type IntMap v = Map Int v
Or we could do it like this:
type IntMap = Map Int
Either way, the IntMap type constructor takes one parameter and that is the type of what the integers will point to.
Make sure that you really understand the distinction between type constructors and value constructors. Just because we made a type synonym called IntMap or AssocList doesn't mean that we can do stuff like AssocList [(1,2),(4,5),(7,9)]. All it means is that we can refer to its type by using different names. We can do [(1,2),(3,5),(8,9)] :: AssocList Int Int, which will make the numbers inside assume a type of Int, but we can still use that list as we would any normal list that has pairs of integers inside. Type synonyms (and types generally) can only be used in the type portion of Haskell. We're in Haskell's type portion whenever we're defining new types (so in data and type declarations) or when we're located after a ::. The :: is in type declarations or in type annotations.
Another cool data type that takes two types as its parameters is the Either a b type. This is roughly how it's defined:
data Either a b = Left a | Right b deriving (Eq, Ord, Read, Show)
It has two value constructors. If the Left is used, then its contents are of type a and if Right is used, then its contents are of type b. So we can use this type to encapsulate a value of one type or another and then when we get a value of type Either a b, we usually pattern match on both Left and Right and we different stuff based on which one of them it was.
ghci> Right 20 Right 20 ghci> Left "w00t" Left "w00t" ghci> :t Right 'a' Right 'a' :: Either a Char ghci> :t Left True Left True :: Either Bool b
So far, we've seen that Maybe a was mostly used to represent the results of computations that could have either failed or not. But somtimes, Maybe a isn't good enough because Nothing doesn't really convey much information other than that something has failed. That's cool for functions that can fail in only one way or if we're just not interested in how and why they failed. A Data.Map lookup fails only if the key we were looking for wasn't in the map, so we know exactly what happened. However, when we're interested in how some function failed or why, we usually use the result type of Either a b, where a is some sort of type that can tell us something about the possible failure and b is the type of a successful computation. Hence, errors use the Left value constructor while results use Right.
An example: a high-school has lockers so that students have some place to put their Guns'n'Roses posters. Each locker has a code combination. When a student wants a new locker, they tell the locker supervisor which locker number they want and he gives them the code. However, if someone is already using that locker, he can't tell them the code for the locker and they have to pick a different one. We'll use a map from Data.Map to represent the lockers. It'll map from locker numbers to a pair of whether the locker is in use or not and the locker code.
import qualified Data.Map as Map data LockerState = Taken | Free deriving (Show, Eq) type Code = String type LockerMap = Map.Map Int (LockerState, Code)
Simple stuff. We introduce a new data type to represent whether a locker is taken or free and we make a type synonym for the locker code. We also make a type synonym for the type that maps from integers to pairs of locker state and code. And now, we're going to make a function that searches for the code in a locker map. We're going to use an Either String Code type to represent our result, because our lookup can fail in two ways — the locker can be taken, in which case we can't tell the code or the locker number might not exist at all. If the lookup fails, we're just going to use a String to tell what's happened.
lockerLookup :: Int -> LockerMap -> Either String Code
lockerLookup lockerNumber map =
case Map.lookup lockerNumber map of
Nothing -> Left $ "Locker number " ++ show lockerNumber ++ " doesn't exist!"
Just (state, code) -> if state /= Taken
then Right code
else Left $ "Locker " ++ show lockerNumber ++ " is already taken!"
We do a normal lookup in the map. If we get a Nothing, we return a value of type Left String, saying that the locker doesn't exist at all. If we do find it, then we do an additional check to see if the locker is taken. If it is, return a Left saying that it's already taken. If it isn't, then return a value of type Right Code, in which we give the student the correct code for the locker. It's actually a Right String, but we introduced that type synonym to introduce some additional documentation into the type declaration. Here's an example map:
lockers :: LockerMap
lockers = Map.fromList
[(100,(Taken,"ZD39I"))
,(101,(Free,"JAH3I"))
,(103,(Free,"IQSA9"))
,(105,(Free,"QOTSA"))
,(109,(Taken,"893JJ"))
,(110,(Taken,"99292"))
]
Now let's try looking up some locker codes.
ghci> lockerLookup 101 lockers Right "JAH3I" ghci> lockerLookup 100 lockers Left "Locker 100 is already taken!" ghci> lockerLookup 102 lockers Left "Locker number 102 doesn't exist!" ghci> lockerLookup 110 lockers Left "Locker 110 is already taken!" ghci> lockerLookup 105 lockers Right "QOTSA"
We could have used a Maybe a to represent the result but then we wouldn't know why we couldn't get the code. But now, we have information about the failure in our result type.
Recursive data structures

As we've seen, a constructor in an algebraic data type can have several (or none at all) fields and each field must be of some concrete type. With that in mind, we can make types whose constructors have fields that are of the same type! Using that, we can create recursive data types, where one value of some type contains values of that type, which in turn contain more values of the same type and so on.
Think about this list: [5]. That's just syntactic sugar for 5:[]. On the left side of the :, there's a value and on the right side, there's a list. And in this case, it's an empty list. Now how about the list [4,5]? Well, that desugars to 4:(5:[]). Looking at the first :, we see that it also has an element on its left side and a list (5:[]) on its right side. Same goes for a list like 3:(4:(5:6:[])), which could be written either like that or like 3:4:5:6:[] (because : is right-associative) or [3,4,5,6].
We could say that a list can be an empty list or it can be an element joined together with a : with another list (that can be either the empty list or not).
Let's use algebraic data types to implement our own list then!
data List a = Empty | Cons a (List a) deriving (Show, Read, Eq, Ord)
This reads just like our definition of lists from one of the previous paragraphs. It's either an empty list or a combination of a head with some value and a list. If you're confused about this, you might find it easier to understand in record syntax.
data List a = Empty | Cons { listHead :: a, listTail :: List a} deriving (Show, Read, Eq, Ord)
You might also be confused about the Cons constructor here. cons is another word for :. You see, in lists, : is actually a constructor that takes a value and another list and returns a list. We can already use our new list type! In other words, it has two fields. One field is of the type of a and the other is of the type [a].
ghci> Empty Empty ghci> 5 `Cons` Empty Cons 5 Empty ghci> 4 `Cons` (5 `Cons` Empty) Cons 4 (Cons 5 Empty) ghci> 3 `Cons` (4 `Cons` (5 `Cons` Empty)) Cons 3 (Cons 4 (Cons 5 Empty))
We called our Cons constructor in an infix manner so you can see how it's just like :. Empty is like [] and 4 `Cons` (5 `Cons` Empty) is like 4:(5:[]).
We can define functions to be automatically infix by making them comprised of only special characters. We can also do the same with constructors, since they're just functions that return a data type. So check this out.
infixr 5 :-: data List a = Empty | a :-: (List a) deriving (Show, Read, Eq, Ord)
First off, we notice a new syntactic construct, the fixity declarations. When we define functions as operators, we can use that to give them a fixity (but we don't have to). A fixity states how tightly the operator binds and whether it's left-associative or right-associative. For instance, *'s fixity is infixl 7 * and +'s fixity is infixl 6. That means that they're both left-associative (4 * 3 * 2 is (4 * 3) * 2) but * binds tighter than +, because it has a greater fixity, so 5 * 4 + 3 is (5 * 4) + 3.
Otherwise, we just wrote a :-: (List a) instead of Cons a (List a). Now, we can write out lists in our list type like so:
ghci> 3 :-: 4 :-: 5 :-: Empty (:-:) 3 ((:-:) 4 ((:-:) 5 Empty)) ghci> let a = 3 :-: 4 :-: 5 :-: Empty ghci> 100 :-: a (:-:) 100 ((:-:) 3 ((:-:) 4 ((:-:) 5 Empty)))
When deriving Show for our type, Haskell will still display it as if the constructor was a prefix function, hence the parentheses around the operator (remember, 4 + 3 is (+) 4 3).
Let's make a function that adds two of our lists together. This is how ++ is defined for normal lists:
infixr 5 ++ (++) :: [a] -> [a] -> [a] [] ++ ys = ys (x:xs) ++ ys = x : (xs ++ ys)
So we'll just steal that for our own list. We'll name the function .++.
infixr 5 .++ (.++) :: List a -> List a -> List a Empty .++ ys = ys (x :-: xs) .++ ys = x :-: (xs .++ ys)
And let's see if it works ...
ghci> let a = 3 :-: 4 :-: 5 :-: Empty ghci> let b = 6 :-: 7 :-: Empty ghci> a .++ b (:-:) 3 ((:-:) 4 ((:-:) 5 ((:-:) 6 ((:-:) 7 Empty))))
Nice. Is nice. If we wanted, we could implement all of the functions that operate on lists on our own list type.
Notice how we pattern matched on (x :-: xs). That works because pattern matching is actually about matching constructors. We can match on :-: because it is a constructor for our own list type and we can also match on : because it is a constructor for the built-in list type. Same goes for []. Because pattern matching works (only) on constructors, we can match for stuff like that, normal prefix constructors or stuff like 8 or 'a', which are basically constructors for the numeric and character types, respectively.
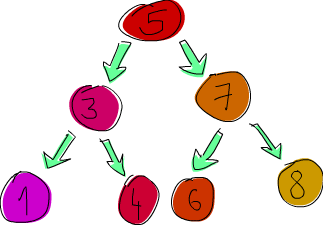
Now, we're going to implement a binary search tree. If you're not familiar with binary search trees from languages like C, here's what they are: an element points to two elements, one on its left and one on its right. The element to the left is smaller, the element to the right is bigger. Each of those elements can also point to two elements (or one, or none). In effect, each element has up to two sub-trees. And a cool thing about binary search trees is that we know that all the elements at the left sub-tree of, say, 5 are going to be smaller than 5. Elements in its right sub-tree are going to be bigger. So if we need to find if 8 is in our tree, we'd start at 5 and then because 8 is greater than 5, we'd go right. We're now at 7 and because 8 is greater than 7, we go right again. And we've found our element in three hops! Now if this were a normal list (or a tree, but really unbalanced), it would take us seven hops instead of three to see if 8 is in there.
Sets and maps from Data.Set and Data.Map are implemented using trees, only instead of normal binary search trees, they use balanced binary search trees, which are always balanced. But right now, we'll just be implementing normal binary search trees.
Here's what we're going to say: a tree is either an empty tree or it's an element that contains some value and two trees. Sounds like a perfect fit for an algebraic data type!
data Tree a = EmptyTree | Node a (Tree a) (Tree a) deriving (Show, Read, Eq)
Okay, good, this is good. Instead of manually building a tree, we're going to make a function that takes a tree and an element and inserts an element. We do this by comparing the value we want to insert to the root node and then if it's smaller, we go left, if it's larger, we go right. We do the same for every subsequent node until we reach an empty tree. Once we've reached an empty tree, we just insert a node with that value instead of the empty tree.
In languages like C, we'd do this by modifying the pointers and values inside the tree. In Haskell, we can't really modify our tree, so we have to make a new sub-tree each time we decide to go left or right and in the end the insertion function returns a completely new tree, because Haskell doesn't really have a concept of pointer, just values. Hence, the type for our insertion function is going to be something like a -> Tree a - > Tree a. It takes an element and a tree and returns a new tree that has that element inside. This might seem like it's inefficient but laziness takes care of that problem.
So, here are two functions. One is a utility function for making a singleton tree (a tree with just one node) and a function to insert an element into a tree.
singleton :: a -> Tree a
singleton x = Node x EmptyTree EmptyTree
treeInsert :: (Ord a) => a -> Tree a -> Tree a
treeInsert x EmptyTree = singleton x
treeInsert x (Node a left right)
| x == a = Node x left right
| x < a = Node a (treeInsert x left) right
| x > a = Node a left (treeInsert x right)
The singleton function is just a shortcut for making a node that has something and then two empty sub-trees. In the insertion function, we first have the edge condition as a pattern. If we've reached an empty sub-tree, that means we're where we want and instead of the empty tree, we put a singleton tree with our element. If we're not inserting into an empty tree, then we have to check some things. First off, if the element we're inserting is equal to the root element, just return a tree that's the same. If it's smaller, return a tree that has the same root value, the same right sub-tree but instead of its left sub-tree, put a tree that has our value inserted into it. Same (but the other way around) goes if our value is bigger than the root element.
Next up, we're going to make a function that checks if some element is in the tree. First, let's define the edge condition. If we're looking for an element in an empty tree, then it's certainly not there. Okay. Notice how this is the same as the edge condition when searching for elements in lists. If we're looking for an element in an empty list, it's not there. Anyway, if we're not looking for an element in an empty tree, then we check some things. If the element in the root node is what we're looking for, great! If it's not, what then? Well, we can take advantage of knowing that all the left elements are smaller than the root node. So if the element we're looking for is smaller than the root node, check to see if it's in the left sub-tree. If it's bigger, check to see if it's in the right sub-tree.
treeElem :: (Ord a) => a -> Tree a -> Bool
treeElem x EmptyTree = False
treeElem x (Node a left right)
| x == a = True
| x < a = treeElem x left
| x > a = treeElem x right
All we had to do was write up the previous paragraph in code. Let's have some fun with our trees! Instead of manually building one (although we could), we'll use a fold to build up a tree from a list. Remember, pretty much everything that traverses a list one by one and then returns some sort of value can be implemented with a fold! We're going to start with the empty tree and then approach a list from the right and just insert element after element into our accumulator tree.
ghci> let nums = [8,6,4,1,7,3,5] ghci> let numsTree = foldr treeInsert EmptyTree nums ghci> numsTree Node 5 (Node 3 (Node 1 EmptyTree EmptyTree) (Node 4 EmptyTree EmptyTree)) (Node 7 (Node 6 EmptyTree EmptyTree) (Node 8 EmptyTree EmptyTree))
In that foldr, treeInsert was the folding function (it takes a tree and a list element and produces a new tree) and EmptyTree was the starting accumulator. nums, of course, was the list we were folding over.
When we print our tree to the console, it's not very readable, but if we try, we can make out its structure. We see that the root node is 5 and then it has two sub-trees, one of which has the root node of 3 and the other a 7, etc.
ghci> 8 `treeElem` numsTree True ghci> 100 `treeElem` numsTree False ghci> 1 `treeElem` numsTree True ghci> 10 `treeElem` numsTree False
Checking for membership also works nicely. Cool.
So as you can see, algebraic data structures are a really cool and powerful concept in Haskell. We can use them to make anything from boolean values and weekday enumerations to binary search trees and more!
Typeclasses 102
So far, we've learned about some of the standard Haskell typeclasses and we've seen which types are in them. We've also learned how to automatically make our own types instances of the standard typeclasses by asking Haskell to derive the instances for us. In this section, we're going to learn how to make our own typeclasses and how to make types instances of them by hand.
A quick recap on typeclasses: typeclasses are like interfaces. A typeclass defines some behavior (like comparing for equality, comparing for ordering, enumeration) and then types that can behave in that way are made instances of that typeclass. The behavior of typeclasses is achieved by defining functions or just type declarations that we then implement. So when we say that a type is an instance of a typeclass, we mean that we can use the functions that the typeclass defines with that type.
Typeclasses have pretty much nothing to do with classes in languages like Java or Python. This confuses many people, so I want you to forget everything you know about classes in imperative languages right now.
For example, the Eq typeclass is for stuff that can be equated. It defines the functions == and /=. If we have a type (say, Car) and comparing two cars with the equality function == makes sense, then it makes sense for Car to be an instance of Eq.
This is how the Eq class is defined in the standard prelude:
class Eq a where
(==) :: a -> a -> Bool
(/=) :: a -> a -> Bool
x == y = not (x /= y)
x /= y = not (x == y)
Woah, woah, woah! Some new strange syntax and keywords there! Don't worry, this will all be clear in a second. First off, when we write class Eq a where, this means that we're defining a new typeclass and that's called Eq. The a is the type variable and it means that a will play the role of the type that we will soon be making an instance of Eq. It doesn't have to be called a, it doesn't even have to be one letter, it just has to be a lowercase word. Then, we define several functions. It's not mandatory to implement the function bodies themselves, we just have to specify the type declarations for the functions.
Anyway, we did implement the function bodies for the functions that Eq defines, only we defined them in terms of mutual recursion. We said that two instances of Eq are equal if they are not different and they are different if they are not equal. We didn't have to do this, really, but we did and we'll see how this helps us soon.
So once we have a class, what can we do with it? Well, not much, really. But once we start making types instances of that class, we start getting some nice functionality. So check out this type:
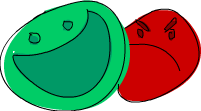
data TrafficLight = Red | Yellow | Green
It defines the states of a traffic light. Notice how we didn't derive any class instances for it. That's because we're going to write up some instances by hand, even though we could derive them for types like Eq and Show. Here's how we make it an instance of Eq.
instance Eq TrafficLight where
Red == Red = True
Green == Green = True
Yellow == Yellow = True
_ == _ = False
We did it by using the instance keyword. So class is for defining new typeclasses and instance is for making our types instances of typeclasses. When we were defining Eq, we wrote class Eq a where and we said that a plays the role of whichever type will be made an instance later on. We can see that clearly here, because when we're making an instance, we write instance Eq TrafficLight where. We replace the a with the actual type.
Because == was defined in terms of /= and vice versa in the class declaration, we only had to overwrite one of them in the instance declaration. That's called the minimal complete definition for the typeclass — the minimum of functions that we have to implement so that our type can behave like the class advertises. To fulfill the minimal complete definition for Eq, we have to overwrite either one of == or /=. If Eq was defined simply like this:
class Eq a where
(==) :: a -> a -> Bool
(/=) :: a -> a -> Bool
we'd have to implement both of these functions when making a type an instance of it, because Haskell wouldn't know how these two functions are related. The minimal complete definition would then be: both == and /=.
You can see that we implemented == simply by doing pattern matching. Since there are many more cases where two lights aren't equal, we specified the ones that are equal and then just did a catch-all pattern saying that if it's none of the previous combinations, then two lights aren't equal.
Let's make this an instance of Show by hand, too. To satisfy the minimal complete definition for Show, we just have to implement its show function, which takes a value and turns it into a string.
instance Show TrafficLight where
show Red = "Red light"
show Yellow = "Yellow light"
show Green = "Green light"
Once again, we used pattern matching to achieve our goals. Let's see how it works in action:
ghci> Red == Red True ghci> Red == Yellow False ghci> Red `elem` [Red, Yellow, Green] True ghci> [Red, Yellow, Green] [Red light,Yellow light,Green light]
Nice. We could have just derived Eq and it would have had the same effect (but we didn't for educational purposes). However, deriving Show would have just directly translated the value constructors to strings. But if we want lights to appear like "Red light", then we have to make the instance declaration by hand.
You can also make typeclasses that are subclasses of other typeclasses. The class declaration for Num is a bit long, but here's the first part:
class (Eq a) => Num a where ...
As we mentioned previously, there are a lot of places where we can cram in class constraints. So this is just like writing class Num a where, only we state that our type a must be an instance of Eq. We're essentially saying that we have to make a type an instance of Eq before we can make it an instance of Num. Before some type can be considered a number, it makes sense that we can determine whether values of that type can be equated or not. That's all there is to subclassing really, it's just a class constraint on a class declaration! When defining function bodies in the class declaration or when defining them in instance declarations, we can assume that a is a part of Eq and so we can use == on values of that type.
But how are the Maybe or list types made as instances of typeclasses? What makes Maybe different from, say, TrafficLight is that Maybe in itself isn't a concrete type, it's a type constructor that takes one type parameter (like Char or something) to produce a concrete type (like Maybe Char). Let's take a look at the Eq typeclass again:
class Eq a where
(==) :: a -> a -> Bool
(/=) :: a -> a -> Bool
x == y = not (x /= y)
x /= y = not (x == y)
From the type declarations, we see that the a is used as a concrete type because all the types in functions have to be concrete (remember, you can't have a function of the type a -> Maybe but you can have a function of a -> Maybe a or Maybe Int -> Maybe String). That's why we can't do something like
instance Eq Maybe where
...
Because like we've seen, the a has to be a concrete type but Maybe isn't a concrete type. It's a type constructor that takes one parameter and then produces a concrete type. It would also be tedious to write instance Eq (Maybe Int) where, instance Eq (Maybe Char) where, etc. for every type ever. So we could write it out like so:
instance Eq (Maybe m) where
Just x == Just y = x == y
Nothing == Nothing = True
_ == _ = False
This is like saying that we want to make all types of the form Maybe something an instance of Eq. We actually could have written (Maybe something), but we usually opt for single letters to be true to the Haskell style. The (Maybe m) here plays the role of the a from class Eq a where. While Maybe isn't a concrete type, Maybe m is. By specifying a type parameter (m, which is in lowercase), we said that we want all types that are in the form of Maybe m, where m is any type, to be an instance of Eq.
There's one problem with this though. Can you spot it? We use == on the contents of the Maybe but we have no assurance that what the Maybe contains can be used with Eq! That's why we have to modify our instance declaration like this:
instance (Eq m) => Eq (Maybe m) where
Just x == Just y = x == y
Nothing == Nothing = True
_ == _ = False
We had to add a class constraint! With this instance declaration, we say this: we want all types of the form Maybe m to be part of the Eq typeclass, but only those types where the m (so what's contained inside the Maybe) is also a part of Eq. This is actually how Haskell would derive the instance too.
Most of the times, class constraints in class declarations are used for making a typeclass a subclass of another typeclass and class constraints in instance declarations are used to express requirements about the contents of some type. For instance, here we required the contents of the Maybe to also be part of the Eq typeclass.
When making instances, if you see that a type is used as a concrete type in the type declarations (like the a in a -> a -> Bool), you have to supply type parameters and add parentheses so that you end up with a concrete type.
Ooh, one more thing, check this out! If you want to see what the instances of a typeclass are, just do :info YourTypeClass in GHCI. So typing :info Num will show which functions the typeclass defines and it will give you a list of the types in the typeclass. :info works for types and type constructors too. If you do :info Maybe, it will show you all the typeclasses that Maybe is an instance of. Also :info can show you the type declaration of a function. I think that's pretty cool.
A yes-no typeclass
In JavaScript and some other weakly typed languages, you can put almost anything inside an if expression. For example, you can do all of the following: if (0) alert("YEAH!") else alert("NO!"), if ("") alert ("YEAH!") else alert("NO!"), if (false) alert("YEAH") else alert("NO!), etc. and all of these will throw an alert of NO!. If you do if ("WHAT") alert ("YEAH") else alert("NO!"), it will alert a "YEAH!" because JavaScript considers non-empty strings to be a sort of true-ish value.
Even though strictly using Bool for boolean semantics works better in Haskell, let's try and implement that JavaScript-ish behavior anyway. For fun! Let's start out with a class declaration.
class YesNo a where
yesno :: a -> Bool
Pretty simple. The YesNo typeclass defines one function. That function takes one value of a type that can be considered to hold some concept of true-ness and tells us for sure if it's true or not. Notice that from the way we use the a in the function, a has to be a concrete type.
Next up, let's define some instances. For numbers, we'll assume that (like in JavaScript) any number that isn't 0 is true-ish and 0 is false-ish.
instance YesNo Int where
yesno 0 = False
yesno _ = True
Empty lists (and by extensions, strings) are a no-ish value, while non-empty lists are a yes-ish value.
instance YesNo [a] where
yesno [] = False
yesno _ = True
Notice how we just put in a type parameter a in there to make the list a concrete type, even though we don't make any assumptions about the type that's contained in the list. What else, hmm ... I know, Bool itself also holds true-ness and false-ness and it's pretty obvious which is which.
instance YesNo Bool where
yesno = id
Huh? What's id? It's just a standard library function that takes a parameter and returns the same thing, which is what we would be writing here anyway.
Let's make Maybe a an instance too.
instance YesNo (Maybe a) where
yesno (Just _) = True
yesno Nothing = False
We didn't need a class constraint because we made no assumptions about the contents of the Maybe. We just said that it's true-ish if it's a Just value and false-ish if it's a Nothing. We still had to write out (Maybe a) instead of just Maybe because if you think about it, a Maybe -> Bool function can't exist (because Maybe isn't a concrete type), whereas a Maybe a -> Bool is fine and dandy. Still, this is really cool because now, any type of the form Maybe something is part of YesNo and it doesn't matter what that something is.
Previously, we defined a Tree a type, that represented a binary search tree. We can say an empty tree is false-ish and anything that's not an empty tree is true-ish.
instance YesNo (Tree a) where
yesno EmptyTree = False
yesno _ = True
Can a traffic light be a yes or no value? Sure. If it's red, you stop. If it's green, you go. If it's yellow? Eh, I usually run the yellows because I live for adrenaline.
instance YesNo TrafficLight where
yesno Red = False
yesno _ = True
Cool, now that we have some instances, let's go play!
ghci> yesno $ length [] False ghci> yesno "haha" True ghci> yesno "" False ghci> yesno $ Just 0 True ghci> yesno True True ghci> yesno EmptyTree False ghci> yesno [] False ghci> yesno [0,0,0] True ghci> :t yesno yesno :: (YesNo a) => a -> Bool
Right, it works! Let's make a function that mimics the if statement, but it works with YesNo values.
yesnoIf :: (YesNo y) => y -> a -> a -> a yesnoIf yesnoVal yesResult noResult = if yesno yesnoVal then yesResult else noResult
Pretty straightforward. It takes a yes-no-ish value and two things. If the yes-no-ish value is more of a yes, it returns the first of the two things, otherwise it returns the second of them.
ghci> yesnoIf [] "YEAH!" "NO!" "NO!" ghci> yesnoIf [2,3,4] "YEAH!" "NO!" "YEAH!" ghci> yesnoIf True "YEAH!" "NO!" "YEAH!" ghci> yesnoIf (Just 500) "YEAH!" "NO!" "YEAH!" ghci> yesnoIf Nothing "YEAH!" "NO!" "NO!"
The Functor typeclass
So far, we've encountered a lot of the typeclasses in the standard library. We've played with Ord, which is for stuff that can be ordered. We've palled around with Eq, which is for things that can be equated. We've seen Show, which presents an interface for types whose values can be displayed as strings. Our good friend Read is there whenever we need to convert a string to a value of some type. And now, we're going to take a look at the Functor typeclass, which is basically for things that can be mapped over. You're probably thinking about lists now, since mapping over lists is such a dominant idiom in Haskell. And you're right, the list type is part of the Functor typeclass.
What better way to get to know the Functor typeclass than to see how it's implemented? Let's take a peek.
class Functor f where
fmap :: (a -> b) -> f a -> f b
Alright. We see that it defines one function, fmap, and doesn't provide any default implementation for it. The type of fmap is interesting. In the definitions of typeclasses so far, the type variable that played the role of the type in the typeclass was a concrete type, like the a in (==) :: (Eq a) => a -> a -> Bool. But now, the f is not a concrete type (a type that a value can hold, like Int, Bool or Maybe String), but a type constructor that takes one type parameter. A quick refresher example: Maybe Int is a concrete type, but Maybe is a type constructor that takes one type as the parameter. Anyway, we see that fmap takes a function from one type to another and a functor applied with one type and returns a functor applied with another type.
If this sounds a bit confusing, don't worry. All will be revealed soon when we check out a few examples. Hmm, this type declaration for fmap reminds me of something. If you don't know what the type signature of map is, it's: map :: (a -> b) -> [a] -> [b].
Ah, interesting! It takes a function from one type to another and a list of one type and returns a list of another type. My friends, I think we have ourselves a functor! In fact, map is just a fmap that works only on lists. Here's how the list is an instance of the Functor typeclass.
instance Functor [] where
fmap = map
That's it! Notice how we didn't write instance Functor [a] where, because from fmap :: (a -> b) -> f a -> f b, we see that the f has to be a type constructor that takes one type. [a] is already a concrete type (of a list with any type inside it), while [] is a type constructor that takes one type and can produce types such as [Int], [String] or even [[String]].
Since for lists, fmap is just map, we get the same results when using them on lists.
map :: (a -> b) -> [a] -> [b] ghci> fmap (*2) [1..3] [2,4,6] ghci> map (*2) [1..3] [2,4,6]
What happens when we map or fmap over an empty list? Well, of course, we get an empty list. It just turns an empty list of type [a] into an empty list of type [b].
Types that can act like a box can be functors. You can think of a list as a box that has an infinite amount of little compartments and they can all be empty, one can be full and the others empty or a number of them can be full. So, what else has the properties of being like a box? For one, the Maybe a type. In a way, it's like a box that can either hold nothing, in which case it has the value of Nothing, or it can hold one item, like "HAHA", in which case it has a value of Just "HAHA". Here's how Maybe is a functor.
instance Functor Maybe where
fmap f (Just x) = Just (f x)
fmap f Nothing = Nothing
Again, notice how we wrote instance Functor Maybe where instead of instance Functor (Maybe m) where, like we did when we were dealing with Maybe and YesNo. Functor wants a type constructor that takes one type and not a concrete type. If you mentally replace the fs with Maybes, fmap acts like a (a -> b) -> Maybe a -> Maybe b for this particular type, which looks OK. But if you replace f with (Maybe m), then it would seem to act like a (a -> b) -> Maybe m a -> Maybe m b, which doesn't make any damn sense because Maybe takes just one type parameter.
Anyway, the fmap implementation is pretty simple. If it's an empty value of Nothing, then just return a Nothing. If we map over an empty box, we get an empty box. It makes sense. Just like if we map over an empty list, we get back an empty list. If it's not an empty value, but rather a single value packed up in a Just, then we apply the function on the contents of the Just.
ghci> fmap (++ " HEY GUYS IM INSIDE THE JUST") (Just "Something serious.") Just "Something serious. HEY GUYS IM INSIDE THE JUST" ghci> fmap (++ " HEY GUYS IM INSIDE THE JUST") Nothing Nothing ghci> fmap (*2) (Just 200) Just 400 ghci> fmap (*2) Nothing Nothing
Another thing that can be mapped over and made an instance of Functor is our Tree a type. It can be thought of as a box in a way (holds several or no values) and the Tree type constructor takes exactly one type parameter. If you look at fmap as if it were a function made only for Tree, its type signature would look like (a -> b) -> Tree a -> Tree b. We're going to use recursion on this one. Mapping over an empty tree will produce an empty tree. Mapping over a non-empty tree will be a tree consisting of our function applied to the root value and its left and right sub-trees will be the previous sub-trees, only our function will be mapped over them.
instance Functor Tree where
fmap f EmptyTree = EmptyTree
fmap f (Node x leftsub rightsub) = Node (f x) (fmap f leftsub) (fmap f rightsub)
ghci> fmap (*2) EmptyTree EmptyTree ghci> fmap (*4) (foldr treeInsert EmptyTree [5,7,3,2,1,7]) Node 28 (Node 4 EmptyTree (Node 8 EmptyTree (Node 12 EmptyTree (Node 20 EmptyTree EmptyTree)))) EmptyTree
Nice! Now how about Either a b? Can this be made a functor? The Functor typeclass wants a type constructor that takes only one type parameter but Either takes two. Hmmm! I know, we'll partially apply Either by feeding it only one parameter so that it has one free parameter. Here's how Either a is a functor in the standard libraries:
instance Functor (Either a) where
fmap f (Right x) = Right (f x)
fmap f (Left x) = Left x
Well well, what did we do here? You can see how we made Either a an instance instead of just Either. That's because Either a is a type constructor that takes one parameter, whereas Either takes two. If fmap was specifically for Either a, the type signature would then be (b -> c) -> Either a b -> Either a c because that's the same as (b -> c) -> (Either a) b -> (Either a) c. In the implementation, we mapped in the case of a Right value constructor, but we didn't in the case of a Left. Why is that? Well, if we look back at how the Either a b type is defined, it's kind of like:
data Either a b = Left a | Right b
Well, if we wanted to map one function over both of them, a and b would have to be the same type. I mean, if we tried to map a function that takes a string and returns a string and the b was a string but the a was a number, that wouldn't really work out. Also, from seeing what fmap's type would be if it operated only on Either values, we see that the first parameter has to remain the same while the second one can change and the first parameter is actualized by the Left value constructor.
This also goes nicely with our box analogy if we think of the Left part as sort of an empty box with an error message written on the side telling us why it's empty.
Maps from Data.Map can also be made a functor because they hold values (or not!). In the case of Map k v, fmap will map a function v -> v' over a map of type Map k v and return a map of type Map k v'.
Try figuring out how Map k is made an instance of Functor by yourself!
With the Functor typeclass, we've seen how typeclasses can represent pretty cool higher-order concepts. We've also had some more practice with partially applying types and making instances. In one of the next chapters, we'll also take a look at some laws that apply for functors.
Kinds and some type-foo

Type constructors take other types as parameters to eventually produce concrete types. That kind of reminds me of functions, which take values as parameters to produce values. We've seen that type constructors can be partially applied (Either String is a type that takes one type and produces a concrete type, like Either String Int), just like functions can. This is all very interesting indeed. In this section, we'll take a look at formally defining how types are applied to type constructors, just like we took a look at formally defining how values are applied to functions by using type declarations. You don't really have to read this section to continue on your magical Haskell quest and if you don't understand it, don't worry about it. However, getting this will give you a very thorough understanding of the type system.
So, values like 3, "YEAH" or takeWhile (functions are also values, because we can pass them around and such) each have their own type. Types are little labels that values carry so that we can reason about the values. But types have their own little labels, called kinds. A kind is more or less the type of a type. This may sound a bit weird and confusing, but it's actually a really cool concept.
What are kinds and what are they good for? Well, let's examine the kind of a type by using the :k command in GHCI.
ghci> :k Int Int :: *
A star? How quaint. What does that mean? A * means that the type is a concrete type. A concrete type is a type that doesn't take any type parameters and values can only have types that are concrete types. If I had to read * out loud (I haven't had to do that so far), I'd say star or just type.
Okay, now let's see what the kind of Maybe is.
ghci> :k Maybe Maybe :: * -> *
The Maybe type constructor takes one concrete type (like Int) and then returns a concrete type like Maybe Int. And that's what this kind tells us. Just like Int -> Int means that a function takes an Int and returns an Int, * -> * means that the type constructor takes one concrete type and returns a concrete type. Let's apply the type parameter to Maybe and see what the kind of that type is.
ghci> :k Maybe Int Maybe Int :: *
Just like I expected! We applied the type parameter to Maybe and got back a concrete type (that's what * -> * means. A parallel (although not equivalent, types and kinds are two different things) to this is if we do :t isUpper and :t isUpper 'A'. isUpper has a type of Char -> Bool and isUpper 'A' has a type of Bool, because its value is basically True. Both those types, however, have a kind of *.
We used :k on a type to get its kind, just like we can use :t on a value to get its type. Like we said, types are the labels of values and kinds are the labels of types and there are parallels between the two.
Let's look at another kind.
ghci> :k Either Either :: * -> * -> *
Aha, this tells us that Either takes two concrete types as type parameters to produce a concrete type. It also looks kind of like a type declaration of a function that takes two values and returns something. Type constructors are curried (just like functions), so we can partially apply them.
ghci> :k Either String Either String :: * -> * ghci> :k Either String Int Either String Int :: *
When we wanted to make Either a part of the Functor typeclass, we had to partially apply it because Functor wants types that take only one parameter while Either takes two. In other words, Functor wants types of kind * -> * and so we had to partially apply Either to get a type of kind * -> * instead of its original kind * -> * -> *. If we look at the definition of Functor again
class Functor f where
fmap :: (a -> b) -> f a -> f b
we see that the f type variable is used as a type that takes one concrete type to produce a concrete type. We know it has to produce a concrete type because it's used as the type of a value in a function. And from that, we can deduce that types that want to be friends with Functor have to be of kind * -> *.
Now, let's do some type-foo. Take a look at this typeclass that I'm just going to make up right now:
class Tofu t where
tofu :: j a -> t a j
Man, that looks weird. How would we make a type that could be an instance of that strange typeclass? Well, let's look at what its kind would have to be. Because j a is used as the type of a value that the tofu function takes as its parameter, j a has to have a kind of *. We assume * for a and so we can infer that j has to have a kind of * -> *. We see that t has to produce a concrete value too and that it takes two types. And knowing that a has a kind of * and j has a kind of * -> *, we infer that t has to have a kind of * -> (* -> *) -> *. So it takes a concrete type (a), a type constructor that takes one concrete type (j) and produces a concrete type. Wow.
OK, so let's make a type with a kind of * -> (* -> *) -> *. Here's one way of going about it.
data Frank a b = Frank {frankField :: b a} deriving (Show)
How do we know this type has a kind of * -> (* -> *) - > *? Well, fields in ADTs are made to hold values, so they must be of kind *, obviously. We assume * for a, which means that b takes one type parameter and so its kind is * -> *. Now we know the kinds of both a and b and because they're parameters for Frank, we see that Frank has a kind of * -> (* -> *) -> * The first * represents a and the (* -> *) represents b. Let's make some Frank values and check out their types.
ghci> :t Frank {frankField = Just "HAHA"}
Frank {frankField = Just "HAHA"} :: Frank [Char] Maybe
ghci> :t Frank {frankField = Node 'a' EmptyTree EmptyTree}
Frank {frankField = Node 'a' EmptyTree EmptyTree} :: Frank Char Tree
ghci> :t Frank {frankField = "YES"}
Frank {frankField = "YES"} :: Frank Char []
Hmm. Because frankField has a type of form a b, its values must have types that are of a similar form as well. So they can be Just "HAHA", which has a type of Maybe [Char] or it can have a value of ['Y','E','S'], which has a type of [Char] (if we used our own list type for this, it would have a type of List Char). And we see that the types of the Frank values correspond with the kind for Frank. [Char] has a kind of * and Maybe has a kind of * -> *. Because in order to have a value, it has to be a concrete type and thus has to be fully applied, every value of Frank blah blaah has a kind of *.
Making Frank an instance of Tofu is pretty simple. We see that tofu takes a j a (so an example type of that form would be Maybe Int) and returns a t a j. So if we replace Frank with j, the result type would be Frank Int Maybe.
instance Tofu Frank where
tofu x = Frank x
ghci> tofu (Just 'a') :: Frank Char Maybe
Frank {frankField = Just 'a'}
ghci> tofu ["HELLO"] :: Frank [Char] []
Frank {frankField = ["HELLO"]}
Not very useful, but we did flex our type muscles. Let's do some more type-foo. We have this data type:
data Barry t k p = Barry { yabba :: p, dabba :: t k }
And now we want to make it an instance of Functor. Functor wants types of kind * -> * but Barry doesn't look like it has that kind. What is the kind of Barry? Well, we see it takes three type parameters, so it's going to be something -> something -> something -> *. It's safe to say that p is a concrete type and thus has a kind of *. For k, we assume * and so by extension, t has a kind of * -> *. Now let's just replace those kinds with the somethings that we used as placeholders and we see it has a kind of (* -> *) -> * -> * -> *. Let's check that with GHCI.
ghci> :k Barry Barry :: (* -> *) -> * -> * -> *
Ah, we were right. How satisfying. Now, to make this type a part of Functor we have to partially apply the first two type parameters so that we're left with * -> *. That means that the start of the instance declaration will be: instance Functor (Barry a b) where. If we look at fmap as if it was made specifically for Barry, it would have a type of fmap :: (a -> b) -> Barry c d a -> Barry c d b, because we just replace the Functor's f with Barry c d. The third type parameter from Barry will have to change and we see that it's conviniently in its own field.
instance Functor (Barry a b) where
fmap f (Barry {yabba = x, dabba = y}) = Barry {yabba = f x, dabba = y}
There we go! We just mapped the f over the first field.
In this section, we took a good look at how type parameters work and kind of formalized them with kinds, just like we formalized function parameters with type declarations. We saw that there are interesting parallels between functions and type constructors. They are, however, two completely different things. When working on real Haskell, you usually won't have to mess with kinds and do kind inference by hand like we did now. Usually, you just have to partially apply your own type to * -> * or * when making it an instance of one of the standard typeclasses, but it's good to know how and why that actually works. It's also interesting to see that types have little types of their own. Again, you don't really have to understand everything we did here to read on, but if you understand how kinds work, chances are that you have a very solid grasp of Haskell's type system.